







If the modifications of the grouped element technique are applied to one of the order 5 asymmetric metasymmetric tiles, even though it has no symmetries, a set of 32 attractors, including the original one, is found, all of which have a similarity dimension of 2. 8 of these generate 6 partial postcomposition derivatives of the symmetric and demisymmetric tiles, and one is disconnected, leaving 23 novel tiles.
8 of the attractors are complex teragons with the same outline as the symmetric tile, but with voids.








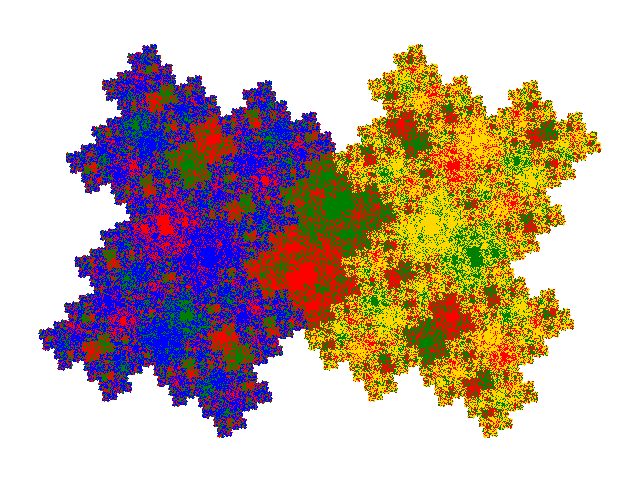
These tiles all have a reather similar appearance. Plotting the weight function makes the differences more obvious.
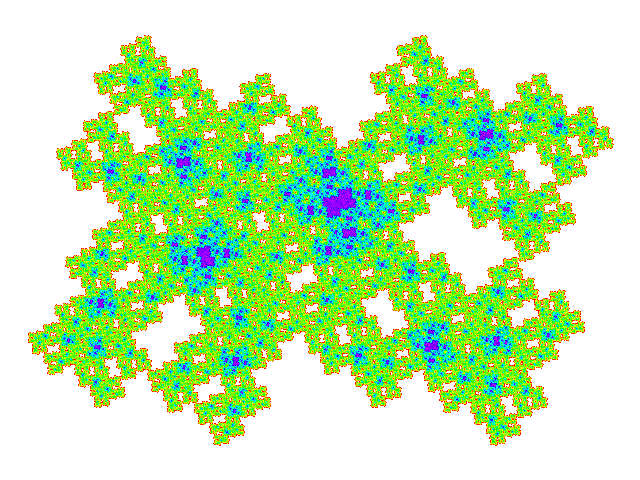
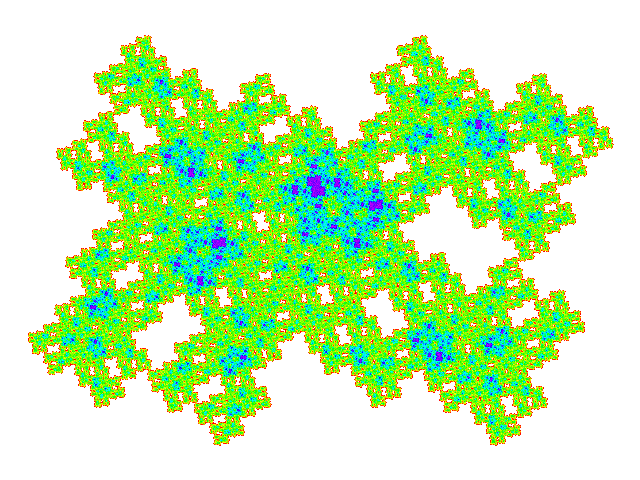
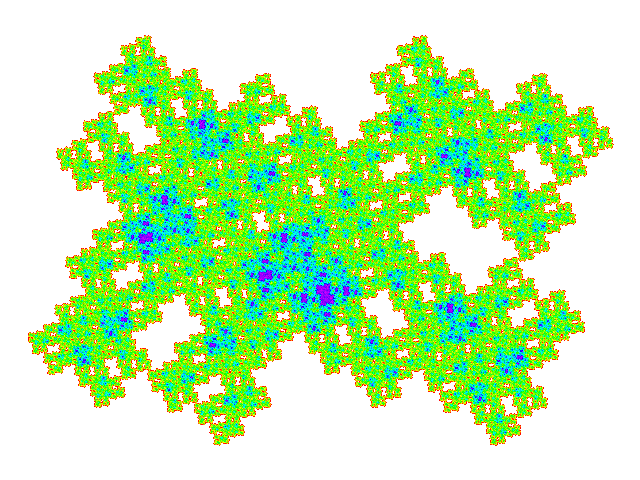
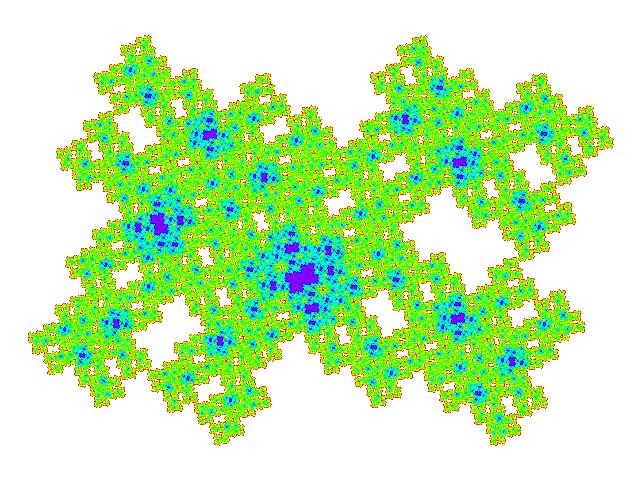
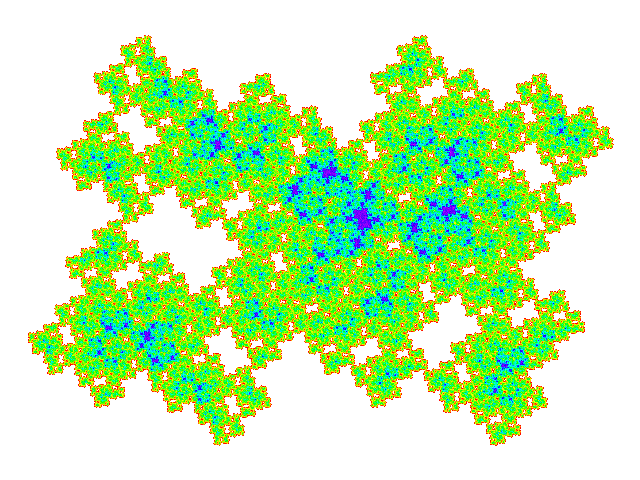
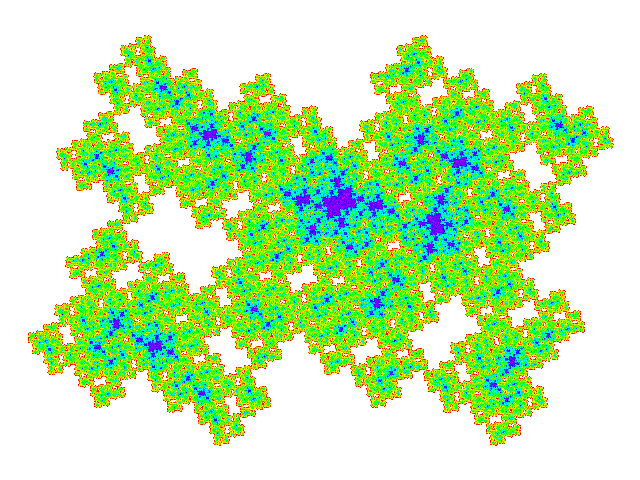
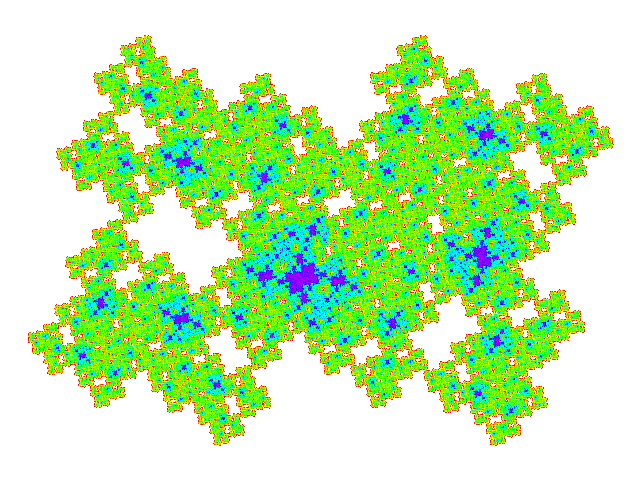
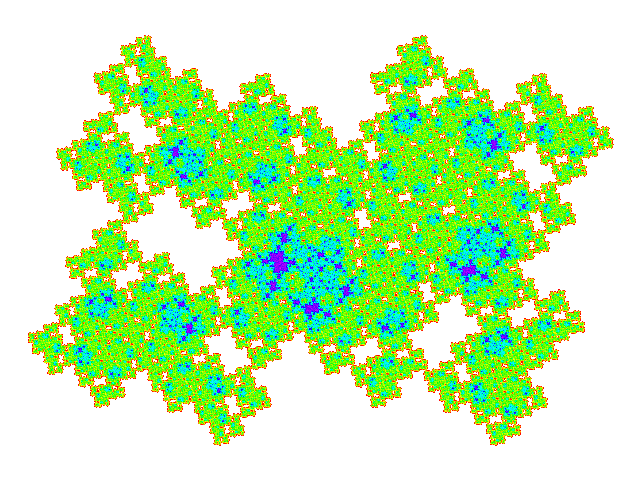
Four copies of these tiles combine to make a symmetric tile, so tilings of these tiles have a multiple of four copies in the unit cell. (Dissecting one of the four copies replaces one copy by five, so dissection doesn't result in exceptions to this rule.) The unit cells are shown below. It is not visually obvious that the four copies don't overlap, but this can be confirmed by plotting the weight function for the unit cell.







© 2015, 2016 Stewart R. Hinsley