
.png)
A 3 element tile potentially has 6 partial postautocomposition derivatives, 3 of order 5 and 3 of order 7. However on the one hand the symmetric tile is 8-fold degenerate - each of its 3 elements can be rotated by 180° - which increase the number of candidates to 48. But on the other hand the same symmetry results in attractors which differ only in orientation, or only in dissection, or in degenerate attractors which occur more than once. The result of this is to produce a total of 3 order 5 tiles (1 symmetric tile and 2 asymmetric tiles) and 5 order 7 tiles (1 symmetric tile and 4 asymmetric tiles.)
The grouped element technique can be applied to the symmetric tiles to produce order 5 and order 7 demimetasymmetric tiles. The co-cell technique can be applied to the asymmetric tiles also producing new order 5 and order 7 tiles. Repeated partial autocomposition leads to order 9, 13, 17, 19, 21, 25, 31 and so tiles.
The symmetric order 5 tile has the dissection polynomial 2c+2c4+c6. It is a complex teragon whose boundary has a countable number of crossing points. It is 32-fold degenerate (8 of these are among the 24 candidate order 5 tiles). It has two copies in the minimal unit cell, with signature 03.

.png)
The asymmetric order 5 tiles have the dissection polynomial c+2c2+c3+c4. Each appears 8 times among the 24 candidate order 5 tiles, the 8 instances forming 4 pairs related by inversion in the origin, each pair having a different dissection. The 4 different dissections - each pair of elements forming a symmetric tile (red/blue, green/cyan) can be rotated by 180° - can be obtained by starting with 4 of the 8 degenerate IFSs for the symmetric tile, or by rotating the red/blue elements around the point -1, and the green/cyan elements around the point 0. The second has an additional 4 dissections obtained by rotating the orange/green/cyan elements around the point (a-1)/(a2-1). (That point is a stationary point (i.e. T(x) = x) of the transform corresponding to the blue element.)

.png)

.png)
The symmetric order 7 tile has the dissection polynomial 4c2+c3+2c4. It is 128-fold degenerate (8 of these are among the 24 candidate order 7 tiles). It has 3 copies in the minimal unit cell, with signature 011.

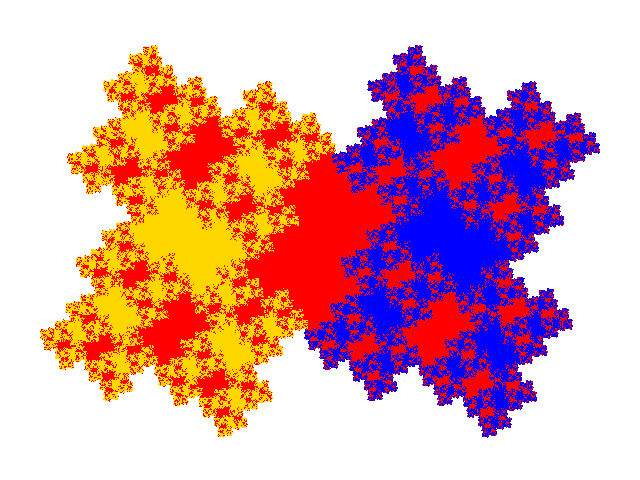
The asymmetric order 7 tiles have the dissection polynomial c+2c2+3c4+c6. Each of these has two dissections - the block of 3 elements making up a symmetric tile can be rotated by 180?. All have them have 3 copies in the minimal unit cell, with signature 013.




The unit cells are shown below.




© 2015, 2016, 2017 Stewart R. Hinsley