
Partial postcomposition is a technique for manipulating an Iterated Function System such that if the similarity dimension of the attractor of the original IFS is 2 then the similarity dimension of the attractor of the modified IFS is also 2. (I suspect that similarity dimension is conserved by this technique, regardless of its value, and the technique could be profitably applied to figures such as the Sierpinski triangle.) This technique can therefore be used to find additional self-similar tiles, given a self-similar tile. Note that while disconnectedness is conserved by this technique, connectness isn't necessarily conserved; hence it is necessary to visually or otherwise check that the resulting attractor is connected.
I have no reason to suspect that the technique does not also work with self-affine tiles.
When I discovered the technique (back in the last millenium) this was the only technique I had for mechanically deriving one tile from another, and I labelled the technique the meta-figure technique, using the sense of meta- as meaning change, as it produces a changed tile. As I have subsequently discovered other techniques such as the grouped element technique and the co-cell technique, which also produce changed tiles, I have since adopted a more tightly descriptive name for the technique, as in the title. I retain the use of the prefix meta- as a less cumbersome way of referring to the figures produced by the technique, both in the general (e.g. metafigure, metatile, metaatractor, metapolygon) and specific (e.g. metaammonite, for the derivatives of the ammonite tile shown below) sense. As there is usually more than one (but, since connectedness is not always conserved, sometimes 0 or 1) derived tile the latter sense usually denotes a set of tiles rather than an individual tile. In some cases, particular the smaller sets, the members of the set can be distinguished by short descriptions. For example the 3 order 5 metapseudoterdragons shown below can be distinguished as the simple, complex and disconnected metapseudoterdragons (one is a simple teragon, one is a complex teragon, and one is a disconnected figure).
Let { Ti } be an IFS. This can be divided into two disjoint non-empty sets { Uj } and { Vk }, i.e. { Uj } ≠ { }, { Vk } ≠ { }, { Uj } ∪ { Vk } ≡ { Ti } and { Uj } ∩ { Vk } ≡ { }. The partial postcomposed IFS is then { Uj } ∪ { Vk.Ti }, i.e. each transform in a subset of the IFS is replaced by the product of itself with each of the transforms of the original IFS.
Clearly the order of the tile is increased by the process. The order of the derived tile is card { Ti } + (card { Ti } - 1) * card { Vk }, i.e. a 2-element tile gives order 3 tiles, a 3-element tile order 5 and 7 tiles, a 4-element tile order 7, 10 and 13 tiles, a 5-element tile order 9, 13, 17 and 21 tiles, and so on.
The number of derived tiles also increases with the increasing order of the base tile. For asymmetric tiles, an 2-element tile has two order 3 derivatives, a 3-element tile three order 5 and three order 7 derivatives, a 4-element tile four order 7, 6 order 10 and 4 order 13 derivatives, a 5-element tile 5 order 9, 10 order 13, 10 order 17 and 5 order 21 tiles, and so on. For symmetric tiles, the number of derivatives is on the one hand decreased by symmetry, and on the other hand increased by the degeneracy of the attractor, and is considered in more, but not exhaustive, detail below.
The ammonite tile is used as an example of the use of the technique on a asymmetric tile, using the x2 + x3 = 1 dissection.

This has two order 3 derivatives. Note that while the ammonite is a simple teragon, only one of the derivatives is a simple teragon, the other being a complex teragon, though in this case as simple as a complex teragon can be. This behaves like connectedness and disconnectedness - a simple teragon can give rise to a complex teragon, but not vice versa. Note also that the tiles have different dissection equations (as is obvious from examination of the construction); the first has the dissection equation x3 + x4 + x5 = 1, and the second x2 + x5 + x6 = 1. (There are circumstances, particular with quadratic Perron tiles, when there is more than one derivative with the same dissection equation.)
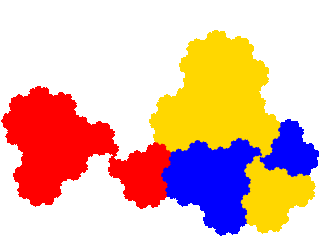

A three element dissection of the ammonite tile, such as the x3 + x4 + x5 = 1 dissection, can also be used as a starting point.
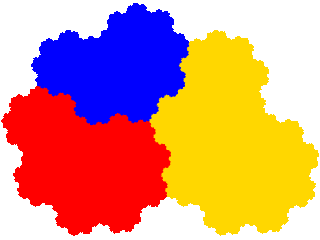
This has three order 5 derivatives. Note that in this case one of resulting attractors (the third) is one of the attractors obtained as an order 3 tile. The general rule is that, if we denote a derived tile as { T*i } and its two subsets as { U*j } and { V*k } then the attractor has a lower order dissection if { Vk } = { V*k }, i.e. if the dissected and post-composed elements are disjoint.
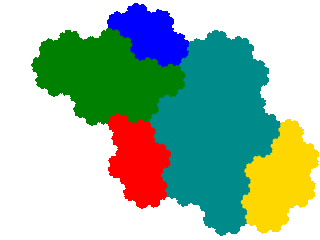
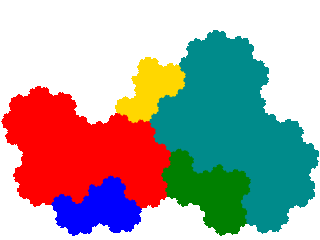

It also has three order 7 derivatives, including a pair of complex teragons with infinite genus.
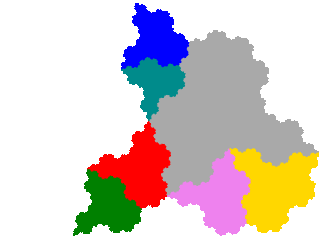


One can perform the technique a second time on the order 3 tiles derived above. As there are two of them, this gives 6 order 5 attractors. Among these we find a couple of disconnected attractors (here homologous to an infinite number of separated discs), so the number of tiles is smaller. My working hypothesis is that all elements adjacent to a particular element n in the original corresponding to elements of { Vk }, is a sufficient but not necessary, condition for the element corresponding to Tn or Tn.Tn (depending on which subset it belongs to) to be separated from the remainder of the attractor.
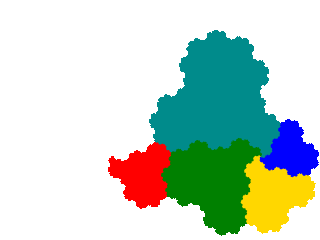
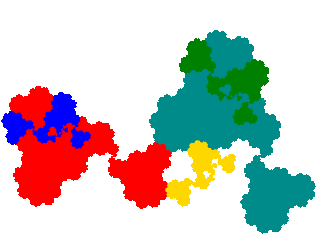
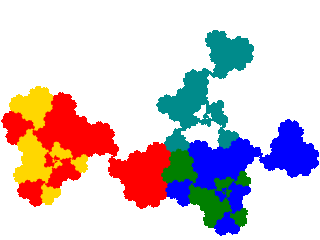



There are also 6 order 7 attractors, which I don't show.
To show the technique applied to an order 4 tile I use the x4 + 2x5 + x6 = 1 dissection of the ammonite tile, which provides an example of two derivatives (here the 2nd and 3rd) with the same dissection equation.
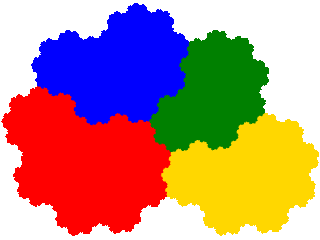
This generates 4 order 7 tiles. The first two of these have already been encountered as order 5 tiles.
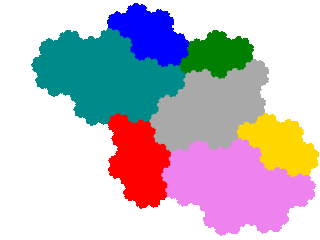
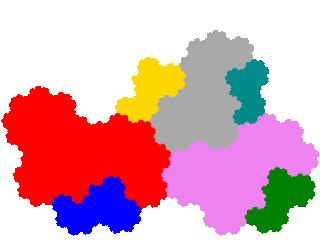
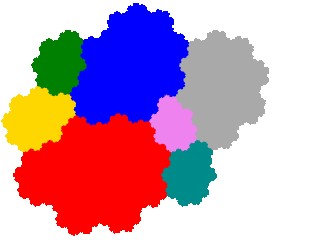

In this instance, as the ammonite tile has two order 2 dissections the other two turn up as order 3 (from x + x5 = 1 dissection) and order 5 (from x2 + x5 + x6 = 1 dissection) tiles respectively.


The original tile is the union of several copies of each derived tile, specifically card { Vk } + 1 copies. If A is the original tile, and A* the derived tile then A ≡ A* ∪ (∪A*.Vk). Consequently if the unit cell for A is ∪ A.Cm then a unit cell for A* is A (∪ A*.Cm) ∪ (∪A*.(Vk.Cm)).
Thus the ammonite tile is made up of two copies of the order 3 derivatives, and as the ammonite tile tiles the plane with signature 0, the order 3 derivatives tile the plane with signatures 02 and 03 respectively.
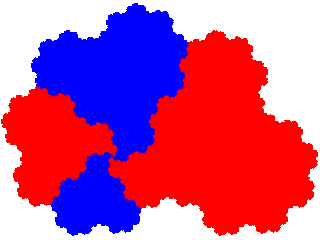

The order 5 derivatives of the order 3 dissection tile the plane with 2 copies in the unit cell, and signatures 04, 05 and 03 respectively.
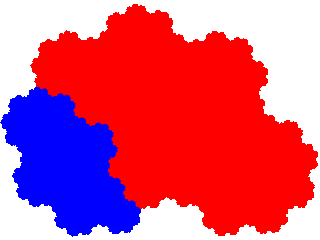


And its order 7 derivatives tile the plane with 3 copies in the unit cell, and signatures 045, 034 and 035 respectively.
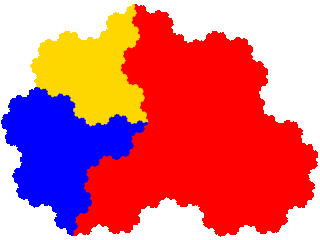


The four tiles among the order 5 derivatives of the order 3 derivatives tile the plane with 4 copies in the unit cell.
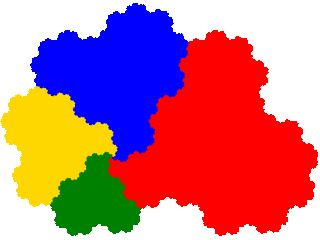
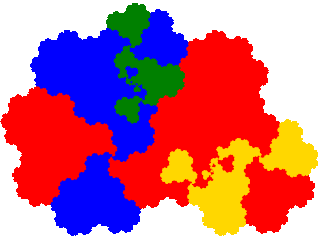
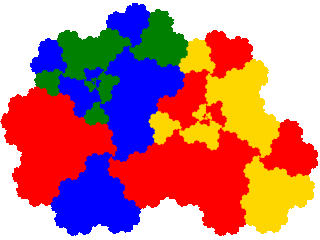

To illustrate derivatives of c2-symmetric tiles the tame twindragon (even orders) and pseudoterdragon (odd orders) are presented below.
The tame twindragon (order 2) is 4-fold degenerate. Thus there are 8 derived IFSs. But the result of symmetry is that the derived attractors are 2-fold degenerate, and the attractors come paired with attractors rotated by 180°, which reduces the number of distinct attractors to 2.


The pseudo terdragon is 8 fold-degenerate, giving 32 derived order 5 IFSs. The attractors are at least 4-fold degenerate, and they again come in rotated pairs, reducing the number to 4, which is further reduced to 3 by the additional degeneracy of the symmetric derivative. (This is 32-fold degenerate, but only 8 of the IFSs are produced by the post-composition technique.) In this case one of the attractors is disconnected.



There are also 32 derived order 7 IFS, which are at least 2-fold degenerate, and again come in rotated pairs, which reduces the number to 8, which is further reduced to 5 by the additional degeneracy of the symmetric (and disconnected) derivative.





The order 4 tame twindragon symmetric dissection is 16-fold degenerate, giving 64 derived order 7 IFSs. The attractors are 8 fold degenerate. The number of distinct attractors is therefore reduced to 4 (2 of which are disconnected).




Generalising, degeneracy is reduced by a factor of 2card { Vk }. If n is the number of distinct derived attractors for an asymmetric tile, for even order tiles the number of distinct attractors is n / 21 + card { Vk } (with an extra power of two for the rotational pairs). The number for odd order tiles is more complicated.
d1-symmetric tiles behave like c2-symmetric tiles, except that the attractors come in mirror image pairs, rather than pairs rotated by 180° with respect to each other. However no order-3 d1-symmetric dissections of a d1-symmetric tile are known offhand.
The right isoceles triangle is used as an example of a d1-symmetric tile. As this is a polygon, the derived tiles are countablegons rather than teragons. The Levy curve would be an alternative example, but as it is a rather cryptic complex teragon the derived tiles would be particularly complex and crypytic - not ideal for illustration.
The order 2 right isoceles triangle gives rise to 2 distinct order 3 attractors, one of which is a a simple countablegon (right isoceles triangular spiral) and one of which is a complex countablegon (single-ended right isoceles triangular rectilinear catenocountablegon).


The symmetric dissection of the order 4 right isoceles triangle gives rise to 4 distinct order 7 attractors, one of which is a simple countablegon, two of which are complex countablegons, and one of which is disconnected.
The fudgeflake is used as an example c3-symmetric tile. As the fudgeflake is 27-fold degenerate there are 81 derived order 5 IFSs. Each attractor is 9-fold degenerate, and they come in rotationally equivalent triplets, so there are only 3 distinct attractors, one of which is disconnected.



There are also 81 derived order 7 IFS. Each attractor is 3-fold degenerate, and comes in rotationally equivalent triplets, so there are 9 distinct attractors, composed of 8 complex teragons and a disconnected attractor.









There is no obvious order 6 c3-symmetric dissection of a tile. There is an order 9 symmetric dissection of the fudgeflake. This has 311 distinct derived order 17 IFSs. But the attractors are 38-fold degenerate, and come in rotationally equivalent triplets, so the number of distinct attractors in 9.
Similar analyses can be done for d3-symmetric tiles (e.g. the order 4 equilateral triangle), c4-symmetric tiles (e.g. the order 5 Mandelbrot quintet), d4-symmetric tiles (e.g the order 4 square), c6-symmetric tiles (e.g. the order 7 flowsnake) and d6-symmetric tile (e.g. the order 7 Koch snowflake).
The area of the derived tile compared to the original can be calculated from the rule used to ascertain the tiling of the original by the derived tile. For tiles based on quadratic Perron numbers the area is a rational fraction of that of the original. For example the order 3 meta tame twindragons are ²⁄₃ of a tame twindragon.
For tiles based on non-quadratic Perron numbers the area is an irrational fraction of the original. For non-Perron tiles the area is usually an irrational fraction of that of the original, but as of the time of writing I can't exclude the possibility that there are exceptions. (For example when the technique is applied the order 2 right-angled triangle - in which the ratio of the area of the two parts can take any value between 0 and 1 exclusive - the ratio of areas of derived and original tiles is rational if the ratio of the areas of the two parts of the tile is rational. For most values of the ratio the order 2 right-angled triangle is a non-Perron tile, but it may be the case that the instances where the ratio is rational are Perron tiles, so I can't be sure that this is not an example of an exception.)
A number of transition rules, showing the tendency of the process to produce more complex attractors, can be stated, including
It is thought that there are other properties (e.g. topological genus) that display similar rules.
Above partial post(auto)composition derivatives of an IFS { Ti } divided into two disjoint non-empty sets { Uj } and { Vk } were defined as IFSs of the form { Uj } ∪ { Vk.Ti }. This leads to the question as to whether there are any circumstances in which we can involve a second IFS { Si } to generate IFSs of the form { Uj } ∪ { Vk.Si }.
There is one case in which we can, but which does not give us anything new. Consider a derived IFS { T'i } ≡ { Uj } ∪ { Vk.Ti }. Rewrite this as { T'i } ≡ { Wm } ∪ { Zn } ∪ { Vk.Ti }, where { Wm } and { Zn } are are again disjoint non-empty sets. Then we can have { T"i } ≡ { Wm } ∪ { Zn.Ti } ∪ { Vk.Ti }. On inspection this can be seen to be equivalent to partial post(auto)composition with a different { Uj } and { Vk }.
The next simplest case is when { Si } and { Ti } are both members of a set of IFSs which generate the same degenerate IFS, i.e. the attractor has the same position, orientation, size and dissection, but the elements have a different set of orientations and/or mirror parities. (This can only be the case for symmetric tiles.) This does not consistently conserve a similarity dimension of 2, but does generate further tiles. For example, applied to the tame twindragon it generates 24 IFSs which include 2 pairs with attractors which are tiles, but also 20 whose attractors are not tiles. The tiles are those that are generated from the meta tame twindragons by the co-cell technique, which may not be coincidence.
While investigating the preceding experimentally, due to an editing error, it was discovered that using appropriately scaled, positioned and oriented IFSs for the tame twindragon and pseudoterdragon, partial postallocomposition generation some tiles among its outputs, with a higher hit rate than is obtained from a polynomial based vector search for tiles of the same order. Like with composition of IFSs identifying the appropriately scaled, posititioned and oriented IFSs is a non-trivial task.
Intermediate between the last two cases above is the situation where the two IFSs have the same attractor, but correspond to different dissections. An experiment with the two dissections order two dissections of the ammonite tile failed to generate tiles, but in the light of the preceding it seems likely that there are cases where it does.
Thus partial post(allo)composition is a subject requiring further investigation.
© 2017 Stewart R. Hinsley