
Partial post(allo)composition is a technique for manipulating an Iterated Function System such that if the similarity dimension of the attractor of the original IFS is 2 then the similarity dimension of the attractor of the modified IFS is also 2. This technique can therefore be used to find additional self-similar tiles, given a self-similar tile. Note that while disconnectedness is conserved by this technique, connectness isn't necessarily conserved; hence it is necessary to visually or otherwise check that the resulting attractor is connected.
It is a generalisation of partial post(auto)composition.
I have no reason to suspect that the technique does not also work with self-affine tiles.
Let { Ti } be an IFS. This can be divided into two disjoint non-empty sets { Uj } and { Vk }, i.e. { Uj } ≠ { }, { Vk } ≠ { }, { Uj } ∪ { Vk } ≡ { Ti } and { Uj } ∩ { Vk } ≡ { }. Let { Si } be a second, different, IFS. The partial postcomposed IFS is then { Uj } ∪ { Vk.Si }, i.e. each transform in a subset of the IFS is replaced by the product of itself with each of the transforms of the second IFS.
Clearly the order of the tile is increased by the process. The order of the derived tile is card { Ti } + (card { Si } - 1) * card { Vk }.
The number of derived tiles also increases with the increasing order of the base tile. For symmetric tiles, the number of derivatives is on the one hand decreased by symmetry, and on the other hand increased by the degeneracy of the attractor.
The technique does not work for arbitrary combinations of IFSs { Si } and { Ti }, so it is desirable to identify the rules that constrain when it does work.
I conjecture that it works for the same combinations of tiles as does composition of IFSs. I conjecture that the tiling vectors of a periodic tiling being the same is a necessary but not sufficient condition.
Two specific general cases have been identified; when{ Si } and { Ti } have the same attractor, and when { Si } is a partial postcomposition derivative of { Ti } (or vice versa). The former case is relatively uninteresting as the result is a higher order dissection of the same attractor.
As the second case can be used to generate a large class of tile it is convenient to have a means of labelling them. I therefore propose to use the prefix allo-, using the sense of allo- as meaning different, to refer to the figures produced by the application of the technique in this case, in both the general (e.g. allofigure, allotile, alloatractor, allopolygon) and specific (e.g. 6th cubic metasymmetric tile) sense. As there is usually more than one (but, since connectedness is not always conserved, sometimes 0 or 1) derived tile the latter sense usually denotes a set of tiles rather than an individual tile.
One of the 6th cubic "external" tiles is used an example of the use of the technique in this circumstance.

If we denote partial post(allo)composition as S⊗T, and a metatile as μT, then we have two sets of order 7 IFSs - μT⊗T and T⊗μT - of order 7. The first has 15 members (postcomposition of 1 of 5 transforms of 1 of 3 order 5 metatiles), and the second 9 members (postcomposition of 1 of 3 transforms by 1 of three order 5 metatiles). However six of the first set - those involving the unmodified member of the metatile - are the same as double partial post(auto)composition derivatives, and I exclude them from the category of allotiles, giving 9 attractors in each set. Writing the transforms of T as Ti, and the composition of those transforms are Tij, the attractors for the first set may be written as
{ T000, T001, T002, T01, T02, T1, T2 } { T00, T010, T011, T012, T02, T1, T2 } { T00, T01, T020, T021, T022, T1, T2 }
{ T0, T100, T101, T102, T11, T12, T2 } { T0, T10, T110, T111, T112, T12, T2 } { T0, T10, T11, T120, T121, T122, T2 }
{ T0, T1, T200, T201, T202, T21, T22 } { T0, T1, T20, T210, T211, T212, T22 } { T0, T1, T20, T21, T220, T221, T222 }
In general this construction gives n2 candidate attractors of order 3n - 2 for an order n base tile.
The second set contains exactly the same IFSs - as a set operator ⊗ appears to be commutative in this situation.
In the case of the tile being as an example one of the 3 metatiles is disconnected, and as disconnectedness is conserved this means that 3 of the above (the last three) can be immediately identified as disconnected. The remaining 6 are

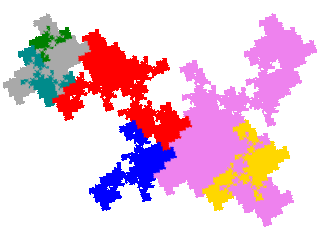




On inspection it can be seen that there are 3 tiles - one a single teragon and the other two complex teragons - and 3 disconnected attractors. Note that the dissection equations for these allotiles are different from the dissection equations for the order 7 metatiles (double partial post(auto)composition derivatives of the original tile).
There are also order 9 tiles, which can be generated in two ways - either as double partial post(allo)compositions derivatives of order 5 metatiles, or as single partial post(allo) composition derivatives of order 7 metatiles. The first set contains 9 elements, and the second set 18 elements.
It turns out that only two of the first set are connected.


Two of the order 7 metatiles are disconnected, so we can eliminate 12 of the second set immediately. Only 1 of the remaining 6 is disconnected, so the second set contributes 5 new tiles.




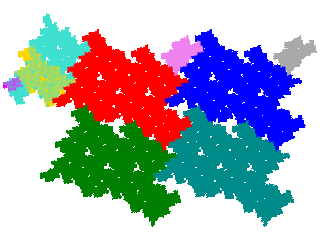
The original tile is the union of several copies of each derived tile. If we write the original tile as { Ti } = { Uj } ∪ { Vk } ∪ { Wl }, the metatile as { Uj } ∪ { Vk.Tm } ∪ { Wl.Tm } and the allotile as { Uj } ∪ { Vk.Tm } ∪ { Wl.Tm.Tn }, then the number of copies is card { Wl } + card { Vk } + 1. If A is the original tile, and A* the derived tile then A ≡ A* ∪ (∪A*.Vk) ∪ (∪A*.Wl). Consequently if the unit cell for A is ∪ A.Cm then a unit cell for A* is A (∪ A*.Cm) ∪ (∪A*.(Vk.Cm)) ∪ (∪A*.(Wl.Cm)).
Thus the unit cells for the order 7 tiles have 3 copies in the unit cell (signature 012).



The order 9 tiles have 4 copies in the unit cell (signatures 0124, 0122, 0112, 0114, 0112, 0112 and 0114 respectively).






TBA.
The area of the derived tile compared to the original can be calculated from the rule used to ascertain the tiling of the original by the derived tile. For tiles based on quadratic Perron numbers the area is a rational fraction of that of the original. For example the order 3 meta tame twindragons are ²⁄₃ of a tame twindragon.
For tiles based on non-quadratic Perron numbers the area is an irrational fraction of the original. For non-Perron tiles the area is usually an irrational fraction of that of the original, but as of the time of writing I can't exclude the possibility that there are exceptions. (For example when the technique is applied the order 2 right-angled triangle - in which the ratio of the area of the two parts can take any value between 0 and 1 exclusive - the ratio of areas of derived and original tiles is rational if the ratio of the areas of the two parts of the tile is rational. For most values of the ratio the order 2 right-angled triangle is a non-Perron tile, but it may be the case that the instances where the ratio is rational are Perron tiles, so I can't be sure that this is not an example of an exception.)
A number of transition rules, showing the tendency of the process to produce more complex attractors, can be stated, including
It is thought that there are other properties (e.g. topological genus) that display similar rules.
Above partial post(auto)composition derivatives of two IFS { Si } and { Ti }, the latter divided into two disjoint non-empty sets { Uj } and { Vk }, were defined as IFSs of the form { Uj } ∪ { Vk.Si }. This leads to the question as to whether partial pre(allo)composition, i.e. the generation of IFSs of the form { Uj } ∪ { Si.Vk }, is a productive technique. It is when { Si } and { Ti } have the same attractor, which is considered under the rubric of dissection. It does not generate new tiles from the combination of a tile and its metatile.
This suggests that the process is not productive, but further investigation is needed before it can be discounted.
© 2017 Stewart R. Hinsley