

There are two known order 3 complex teragons, in addition to the windowed tile. A 3 element tile potentially has 6 partial postautocomposition derivatives, 3 of order 5 and 3 of order 7. Thus these two tiles give rise to 12 candidate attractors. However 3 of these are not connected, leaving 9 tiles - 5 order 5 tiles and 4 order 7 tiles.
The first complex teragon gives rise to two order 5 tiles and two order 7 tiles. The order 5 tiles have the dissection polynomial 2c+2c4+c6.


The minimal unit cells (shown below) have 4 copies, and have the same
footprint as the unit cell of the complex teragon. When the IFS for the complex
teragon is { p→ap; p→ap + 1;
p→-a3p + 1 + a + a2 } the cell
transforms for the first are { p→p;
p→-p; p→ap; p→-ap }.
The cell transforms for the second are { p→p;
p→-p; p→ap + 1; p→-ap
- 1 }.


The order 7 tiles have the dissection polynomials 4c2+c3+2c4 and c+2c2+3c4+c6.
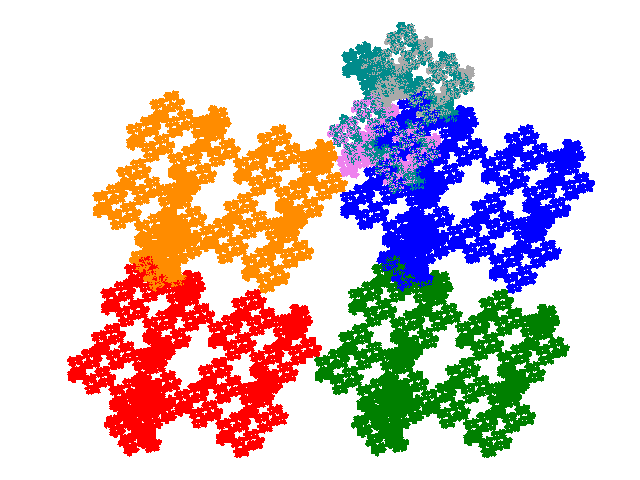

The minimal unit cells (shown below) contain 6 copies of the tile. They are
too complex for the cell transforms to be easily identified by visual
inspection combined with some trial and error. However the heuristic that the
set of cell transforms is the union of the cell transforms for the
corresponding pair of order 5 tiles turns out to work. (This may turn out to be
handy for working out the unit cells for order 13, 17 and 21 tiles, provided
that those for order 9 tiles are accessible.) This has been confirmed by
plotting the weight function for the unit cells. The cell transforms for the
first tile are { p→p; p→-p;
p→ap; p→-ap; p→ap + 1;
p→-ap - 1 }. The cell transforms for the second are {
p→p; p→-p; p→ap;
p→-ap; p→a3p + 1 + a +
a2; p→-a3p - 1 - a -
a2 }. (The last two here come from the disconnected figure
which is the 3rd order 5 partial postcomposition derivative.)


The second complex teragon gives rise to three order 5 tiles and two order 7 tiles.

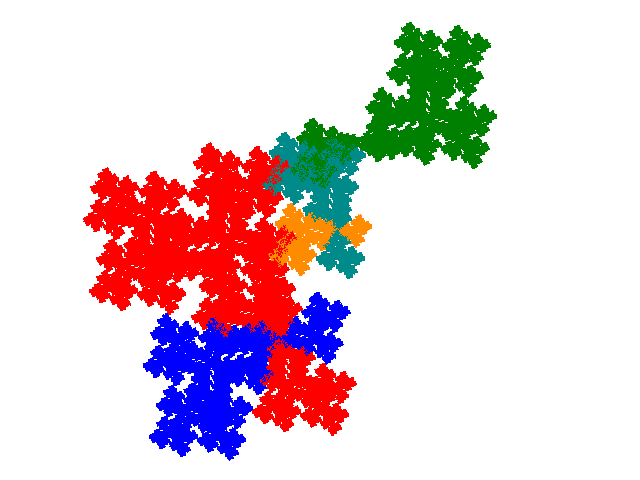

The order 7 tiles have the dissection polynomials 4c2+c3+2c4 and c+2c2+3c4+c6.

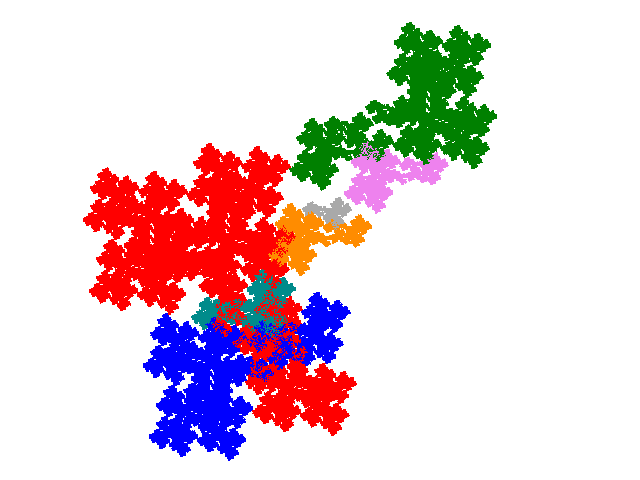
© 2015, 2016 Stewart R. Hinsley