

While all cubic tiles are teragons (with an uncountably infinite number of edges), of the eight known order 3 6th unit cubic tiles the complex teragon has the most complex structure. Five of the tiles - the symmetric (8-fold degenerate), (two) external and (two) demi-symmetric tiles are simple teragons with non-self-approaching boundaries of relatively low dimension The windowed tile (2 dissections), while technically a complex teragon, is composed of a spiral of diminishing copies of the symmetric tile. In contrast the other two complex teragons have boundaries of greater dimension which approach themselves at an infinite number of points, with appreciable parts of the tile composed of fractally intermixed parts of 2 elements.
The first complex teragon was found with IFS { p →
-a3p; p → ap + 1; p → ap + 1
+ a-1 } during a heuristic directed survey. A more convenient
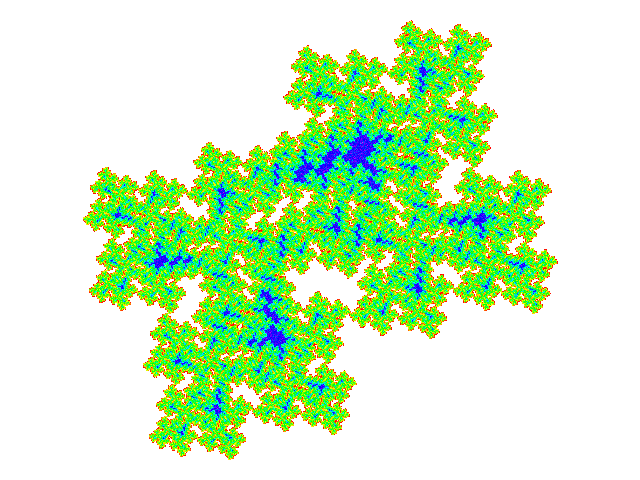
IFS, the attractor for which is shown below, is { p → ap;
p → ap + 1; p → -a3p + 1 +
a1 + a2 }.


The second complex teragon was also found during a heuristic directed
survey, with IFS { p → -p; p → ap + 1;
p → a3p + (1 + a) / 2 }

For the first there are two tilings with signature 00 (two equal
sized copies of the tile making up a unit cell). For the attractor shown above
the cell transforms are { p → p; p →
-p } and { p → p; p → -p +
1 }. The unit cells are shown below.


The tiling vectors for the first unit cell are 2 +
a and 2 and -a-1.


It is likely that there are tilings with more complicated unit cells, containing copies of different sizes, but the complex nature of this teragon makes it difficult to identify the correct position of copies.
The second has a tiliing with a unit cell with signature 00, cell transforms { p → p + a + (a2 - 1)/2; p → -p }, and tiling vectors (3 + a) / 2 and (a-3 - a-2) / 2


© 2015, 2016, 2017 Stewart R.Hinsley