Order 4 Rectifiable Polyominoes and Polyplets
There are two classes of order 4 rectifiable polyominoes and polyplets - those
in which four copies of the figure can be combined to make a square, and those
in which four copies can be combined to make a rectangle.
Order 4 Square Rectifiable Polyominoes and Polyplets
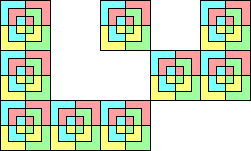
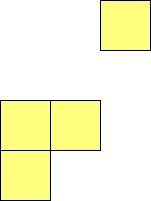
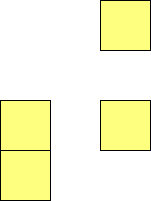
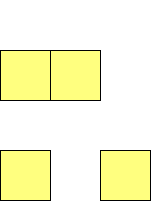
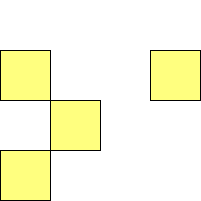
A n-polyomino or polyplet for which 4 copies form a square is a
rep-4n-tile, as 4 copies make up a square, and n squares make up
the polyomino or polyplet.
There are several constraints which we can apply to identify which
polyominoes fall into this category.
- Firstly, as the square has to be divided equally into 4, it must be a
2×2, 4×4, 6×6, 8×8, etc square, and hence n must be 1, 4, 9, 16
etc.
- Secondly the square is divided into square annuli 1 square wide, of which
the polyomino or polyplet much occupy 1 square of the inner annulus, 3
squares of the next one, 5 of the next, and so on.
- Thirdly the squares occupied in each annulus must be consecutive.
- Fourthly the squares occupied in successive annuli must have at least one
edge (for polyominos)
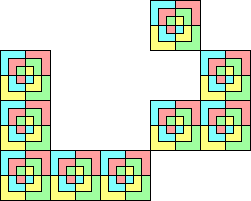
The rules for polyplets are less strict.
- The 3rd rule becomes that, if the squares in an annulus are numbered
consecutively from 0 to 4k-1, then the position of each occupied
square modulo k must be unique.
- The 4th rule is modified to allow contact by corners as well as edges.
(Due to the relaxation of the 3rd rule the implementation details are
considerably complicated.)
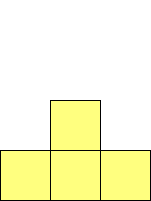
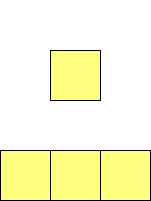
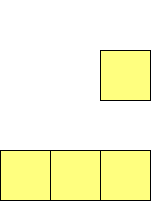
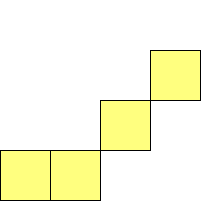
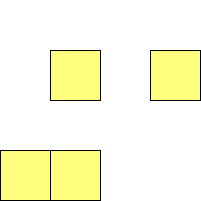
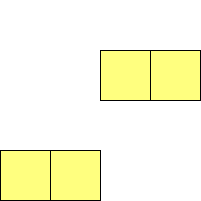
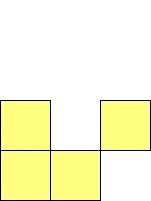
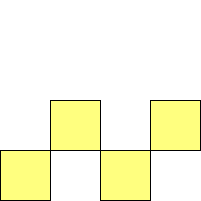
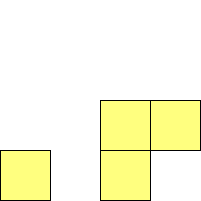
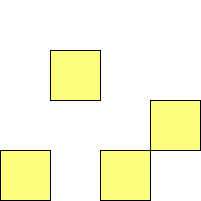
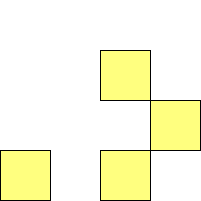
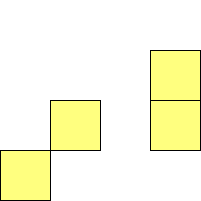
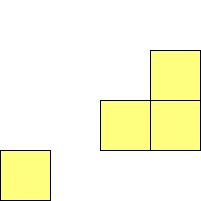
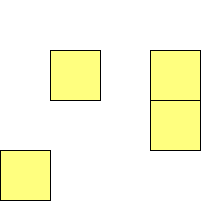
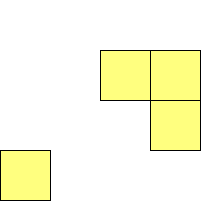
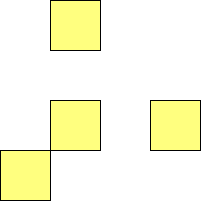
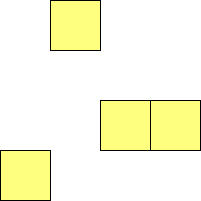
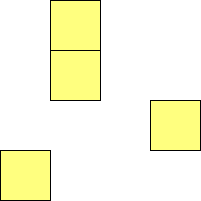
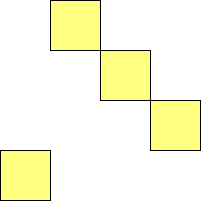
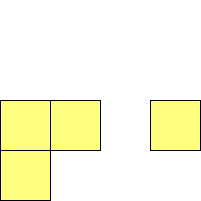
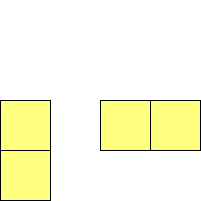
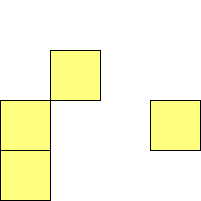
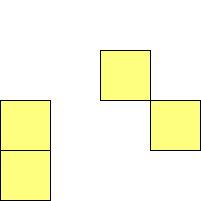
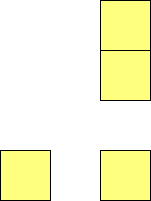
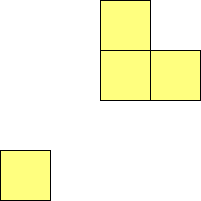
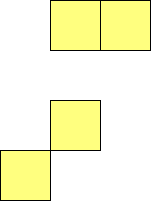
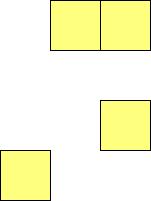
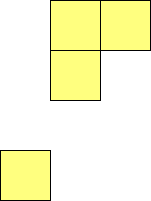
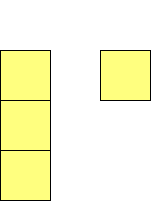
For n=1 there is only one polyomino, the square or monomino.
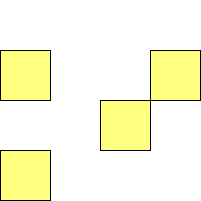
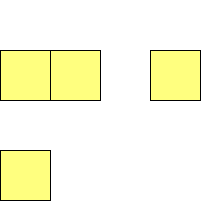
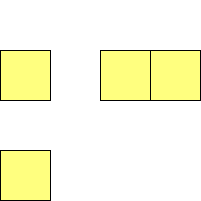
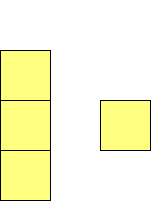
For n=4 there are 3 polyominos - the T-, L- and O-tetrominoes, and 4
polyplets
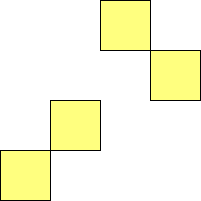
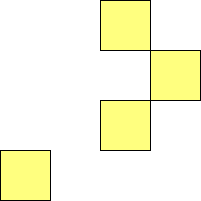
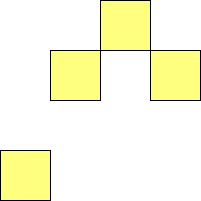
For n=9 there are 23 polyominos.








* *
* *
* *
*
*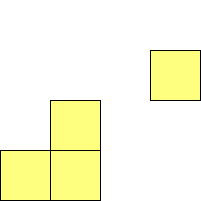 *
* *
* *
*
* *
* *
* *
*
* *
* *
* *
*
* *
* *
* *
*
* *
* *
* *
*
* *
* *
* *
*
* *
* *
* *
*
* *
* *
* *
*
* *
* *
* *
*
* *
* *
* *
*
* *
* *
* *
*
* *
* *
* *
*
* *
* *
* *
*
* *
* *
* *
*
* *
* *
* *
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*