


While laying out elements in a triangular array is at first sight an obvious means of investigating hextal tiles, it turns out to be non-productive. While the smallest triangle does produce a tile (the fudgeflake), many of the larger triangles have invalid numbers of elements, and even those which do have valid numbers of elements don't appear to generate tiles, at least with all the elements having the same orientation. This perhaps not surprising - the attractors approach a triangle, and a triangle needs two copies, one rotated by 180° with respect to the other, to tile the plane, suggesting that any tiles with a high number of elements will also have mixed orientations of elements.
However one can lay out two triangular arrays, with the elements of one lying in the interstices of the elements of the other. In the case there is a simple rule which can be adopted for assigning the orientations of the elements - all elements in one array have the same orientation. When one array is one size smaller than the other the number of elements is n2, which is always a valid number of elements; when it is two sizes smaller the number of elements is n2-n+1, which is also always a valid number of elements. Bigger differences in sizes tend not to give a valid number of elements, or to produce an obvious tile when they do. (If the two arrays are laid out with a common centre, to retain c3-symmetry, then if the difference is sizes is a multiple of 3, the elements of the smaller triangle are superimposed on those of the larger, rather than lying in their interstices, so in that case, if the elements of the two arrays also have the same orientation, the attractor is obviously not a tile.)
When implementing this construction the obvious approach is to use the Eisenstein integers e10 and e01 for the spacing of the elements of the arrays. However that leaves the position of the interstitial elements not being Eisenstein integers, which results in complicating tilings with fractions. This can be addressed by using spacings of e30 and e03. However rotating the array by 90° and using spacings of e12 and e21 turns out to be more convenient for consistency with the constructions used for other fractals.
[Note that the complex number a used in the description of IFSs, etc, below, depends on the rep-number n of the fractals - it is the inversion in the unit circle of the Eisenstein integer of magnitude √n with the smallest imaginary part. (For most small n there is only zero or one such Eisenstein integer.)]
The triangular interstitial hextals are a generalisation of the cyclic tetrahextals, which are the 4-element tiles where the elements are located at e00, e10, e01 and -e11, with the last 3 elements having the same orientation. In the specific case of the cyclic tetrahextals all 4 possible orientations generate tiles.
The IFS
{ p → ap; p → ap + e10; p → ap + e01; p → ap - e11 }
generates what I call the pseudo-Sierpinski triangle, which I denote as P (or P1). This tiles the plane with one copy in the unit cell, and tiling vectors e20 and e22.



The IFS
{ p → -ap; p → -ap + e10; p → -ap + e01; p → -ap - e11 }
generates a tile which is known as the Eisenstein fraction, which I denote as E (or E1). This also tiles the plane with one copy in the unit cell, and tiling vectors e20 and e22.



The IFS
{ p → -ap; p → ap + e10; p → ap + e01; p → ap - e11 }
generates a rep-4-triangle, which I denote T1. This tiles the plane with two copies in the unit cell, and tiling vectors e40 and e24. The unit cell is { p → p; p → -p + e22 }


The IFS
{ p → -ap; p → -ap + e10; p → -ap + e01; p → -ap - e11 }
generates a tile which looks like a skinny version of the Eisenstein fraction, and for the lack of a better idea I denote this A1 (A for anti-triangle.) There is a tiling with two copies in the unit cell, with tiling vectors e20 and e22 and unit cell { p → p; p → -p }, or { p → p; p → p }.
I haven't completely excluded the possibility of a tiling with one copy in the unit cell. However the obvious one-dimensional row tiling, with tiling vector e10, requires the elements in the flanking rows to be reflected to fit into the gaps, which is suggestive that a tiling with one copy in the unit cell is not possible.



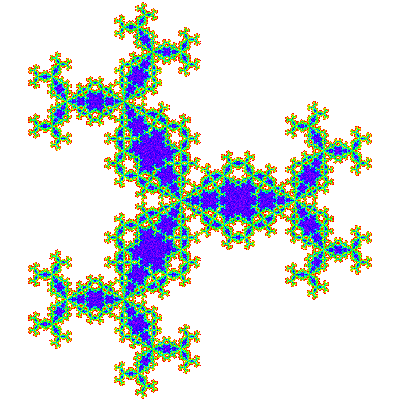


Copies of this tile can be combined to make additional visually attractive images.
The triangle generalises for all sizes of triangular arrays, giving the rep-n2-triangles, denoted Tn-1. These aren't particular interesting in themselves, as they have the same attractor as T1, and consequently the same tiling properties, but they do have different derivatives produced by the grouped element, partial postautocomposition and composition techniques.




The "anti-triangle" also generalises, but not for all sizes of triangular arrays. When denoted An, n modulo 3 must be 0 or 1. This parallels the situation with the starflakes and alterflakes, which also have a common construction which only generates tiles when n modulo 3 is 0 or 1. The other two cyclic tetrahextals don't generalise, probably for similar reasons as for the non-interstitial triangular array.
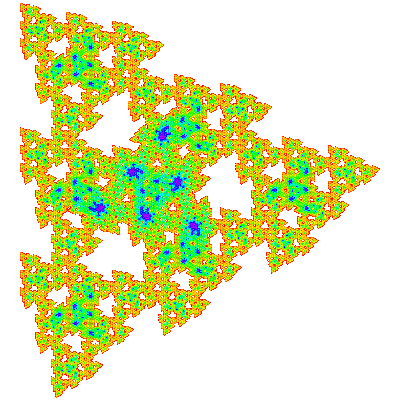
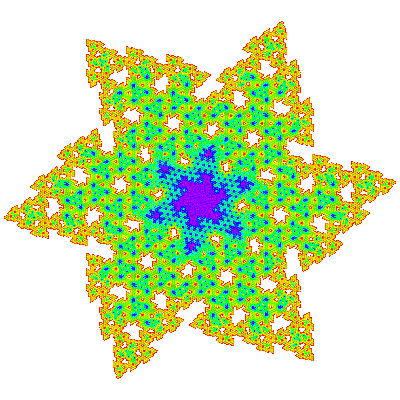
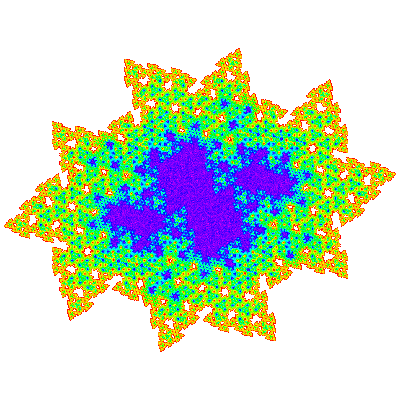
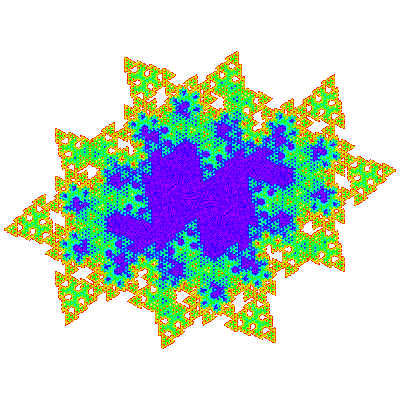
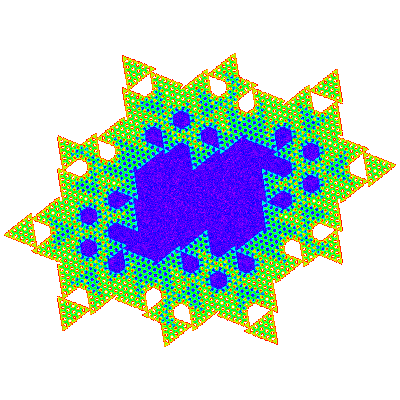
A3, A4, A6 and A7 are shown below.




From the visual appearance working out a tiling for these is intimidating, but it turns out that A3 = A1.T1 and A7 = A1.T1.T1. (If this pattern holds A15 = A1.T1.T1.T1, A31=A1.T1.T1.T1.T1, etc.) Applying empirical rules from the composition of tiles, this leads to the conclusion that the unit cell is { p → p; p → -p }, or { p → p; p → p } and the tiling vectors are those of A1 multiplied by the difference in size, i.e (n+1)e10 and (n+1)e11, and one can guess that the same applies to A4, A6 and other An. This has been confirmed by experiment for A4, A6and A9. (Due to the nature of the boundary of the unit cell, the rendering of a 2×2 patch of a tiling as shown below is not particularly convincing, but that it is a tiling can be confirmed by plotting the measure function, and by rendering larger patches.)
[The construction of An by composition can be rewritten as A3 = A1.T1, A7 = A1.T3, A15 = A1.T7, A31 = A1.T15, etc. This leads to speculation as to whether other composites of cyclic tetrahextals are also constructable as triangular interstitial hextals.]




When the smaller array is two sizes smaller, tiles are also generated. In this case the order is not n2, with the result that the symmetry is cyclic rather than dihedral. The smallest construction here has 7 elements, and has tiles analogous to E and P, denoted E2 and P2.
E2 has the IFS
{ p → -ap; p → -ap + -e11; p → -ap - e10; p → -ap - e01; p → -ap + e20; p → -ap + e02; p → -ap - e22 }
and P2 the IFS
{ p → ap; p → ap + e11; p → ap - e10; p → ap - e01; p → ap + e20; p → ap + e02; p → ap - e22 }

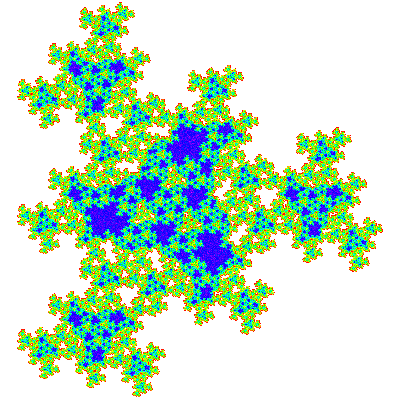
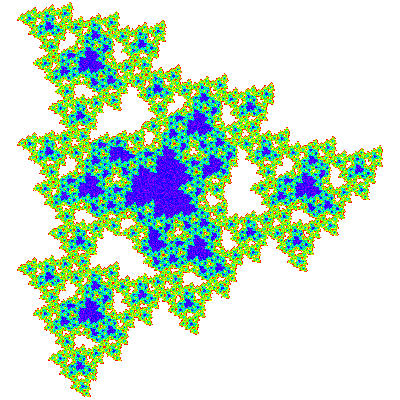
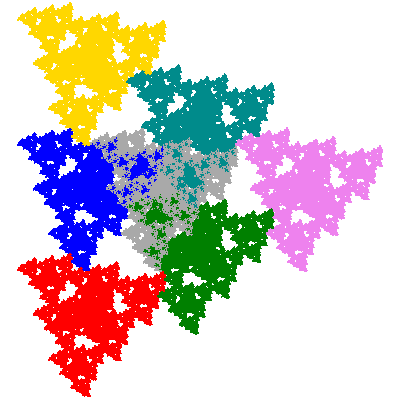
While it is obvious that these tile the plane, it is less obvious how they do so. (Visually one can't identify the holes that would be filled by the solid areas of the attractor.) After a few false starts I zoomed in on the inner area of P2 to see how further dissected elements fitted together, and from this deduced that it tiles the plane with one copy in the unit cell, and that the tiling vectors for the full sized copy are e10/a and e11/a, which turn out to be e20 - e01 and e32. The same vectors were then shown experimentally to also work for E2. With hindsight these numbers could just have been taken from the tiling for T*1 (see below), which while not in itself anymore obvious could be inferred from the tilings of T*n in general.

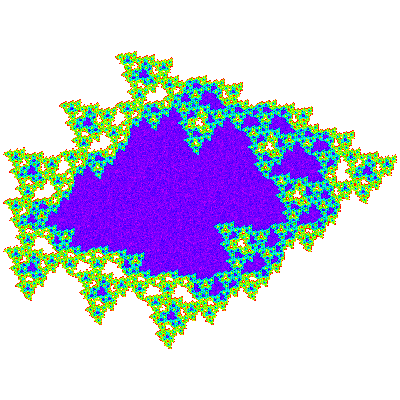
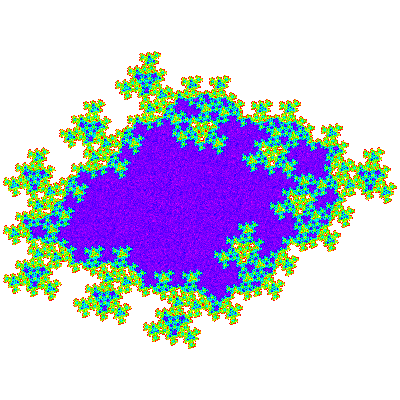

As these are not dihedrally symmetric distinct trans-tiles exist, denoted E2 and P2.

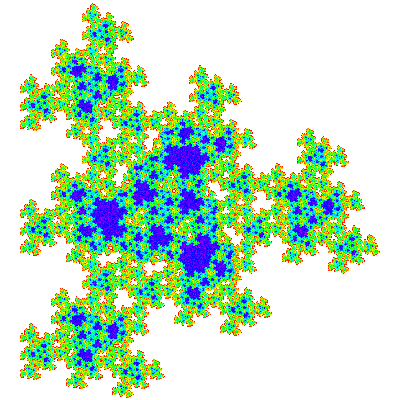
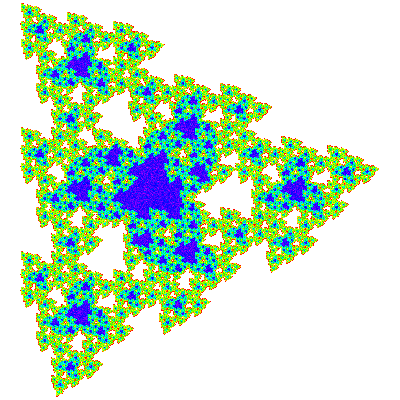
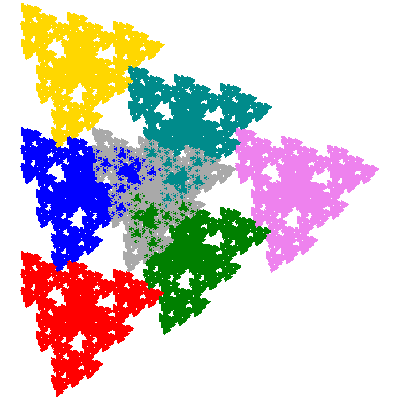
These also tile the plane in the same way.

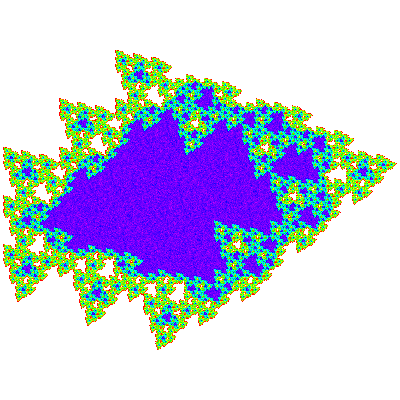
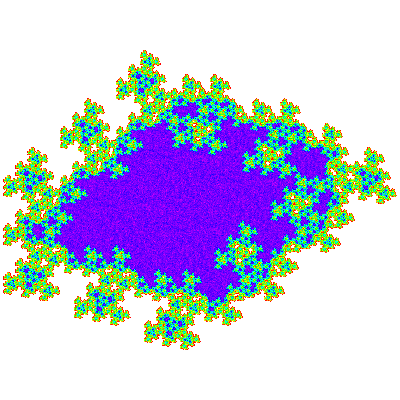

There are another 4 heptahextals produced by this construction A*1, A*1, T*1 and T*1. As these generalise to larger triangular arrays consideration of these is deferred to the next section.
It is observed that E2 has the same outline as A*1 and E2 has the same outline as A*1, and also that P2 has the same outline as T*1 and P2 has the same outline as T*1.
In the case of 7 elements, the group of 6 elements can be split into two groups of 3 which can be orientated independently, but this does not generate any additional tiles.
The general case when the interstitial triangle is two sizes smaller has analogs to An, denoted A*n, for all sizes, and to Tn when n modulo 3 is 1 or 2.
The A*n are visually obvious tiles, with the exception of A*1, but this can be readily confirmed as a tile by plotting its unit cell or a tiling patch, using same construction as for the others.








These all clearly tile the plane with two copies in the unit cell, though it takes a little while to work out the vectors involved. The tiling vectors are (n+2)e21 - e12 and (n+2)e12 - e21, and the unit cell is { p → p; p → -p + (n+1)e11 + e10 }








There are corresponding trans-tiles.








These tile the plane in the same way.








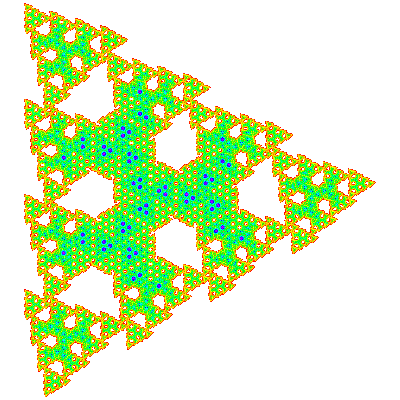
The T*n are not visually obvious, but combining a copy with a copy rotated by 180° to form a candidate unit cell produces a more convincing figure, which can be confirmed by producing a tiling patch. The tiling vectors are (n + 1) * e11 + e10 and (n + 1) * e10 - e01 and the unit cell { p → p; p → -p} or or { p → p; p → p }. Tiles only exist when n % 3 ≠ 0. T*1, T*2 and T*4 are shown below.
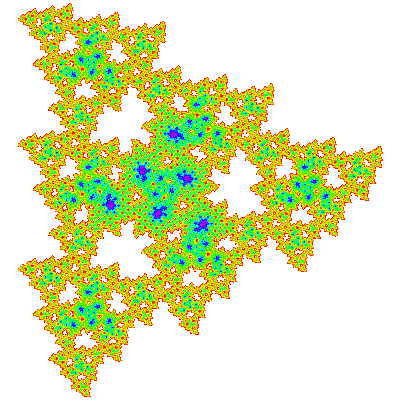
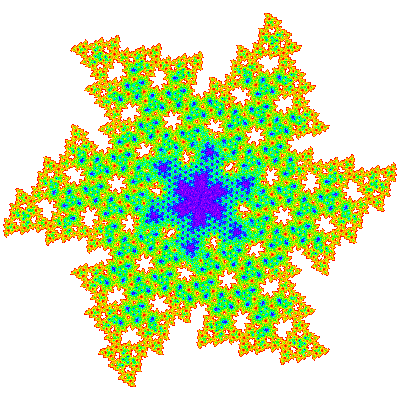
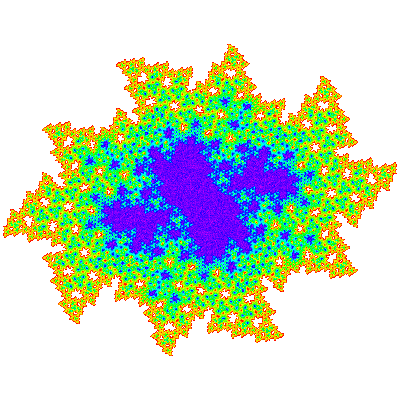



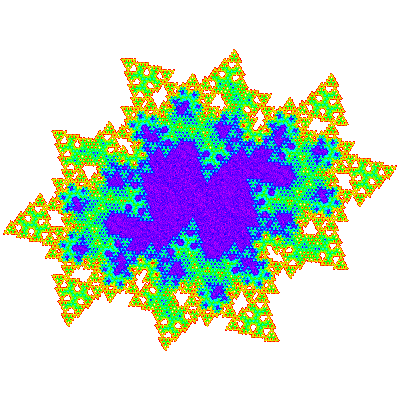



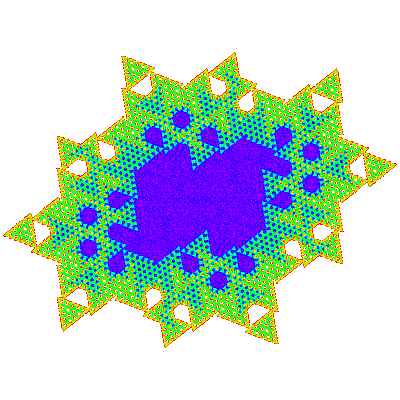

As these are not dihedrally symmetric there are corresponding trans-tiles which tile the plane in the same way.






© 2000, 2018 Stewart R. Hinsley