



If the flowsnakes were not degenerate symmetry would reduce the number of order 13 partial postcomposition derivatives to 2. However as the tiles are degenerate the number is greater. In spite of the tiles being 67- (279,936-) fold degenerate, the breaking of symmetry only results in 7 distinct attractors, 3 of which are not connected.




There is a second set of 4 trans-tiles.




They all tile with plane with two copies in the unit cell, with the tiling vectors as for the flowsnakes.








The next set of partial postcomposition derivatives are order 19. One would expect that the further breaking of symmetry would lead to be a 3-fold number, but a greater proportion are disconnected, and there are just 4 tiles.




And 4 trans- tiles.


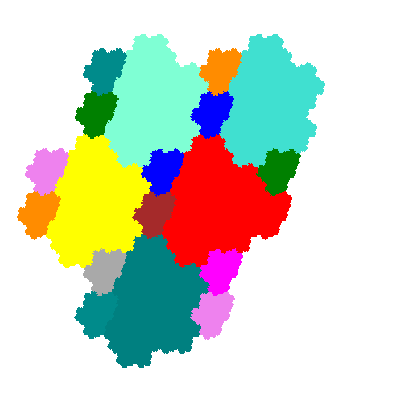

They all tile with plane with three copies in the unit cell, with the tiling vectors as for the flowsnakes.
It has been noticed that grouped element technique can be applied to partial post-composition derivatives of symmetric tiles as if the derivatives were themselves symmetrical. With 13 or 19 elements, and a basal c6-symmetry, this leads to a huge number of candidate attractors, but a large proportion are not connected, and the number of the remainder is reduced by symmetry. The number of tiles so generated does however remain large. It is not obvious that these tiles are distinct from the partial post-composition derivatives of the grouped element derivatives of the parent flowsnakes.
Note that two of the order 19 tiles are c2-symmetric, which gives access to a smaller, more productive, subset of the grouped element derivatives.
Source: Independent discovery
References: