Pacmen Tiles

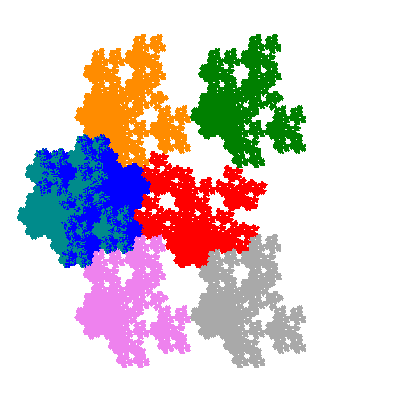
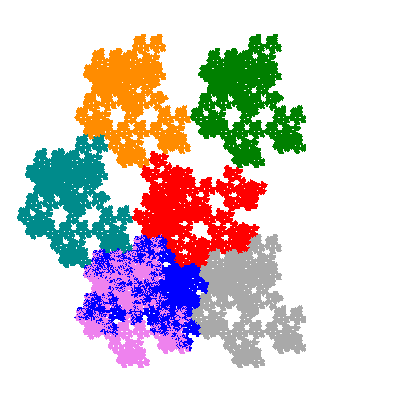
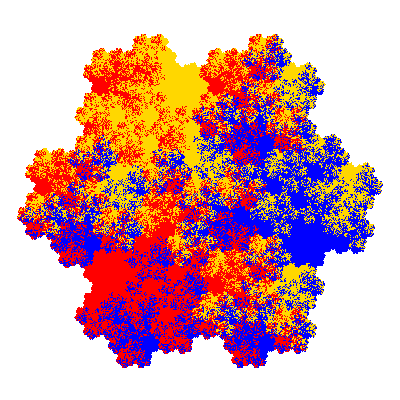
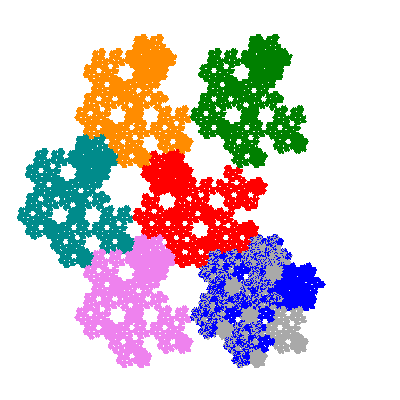
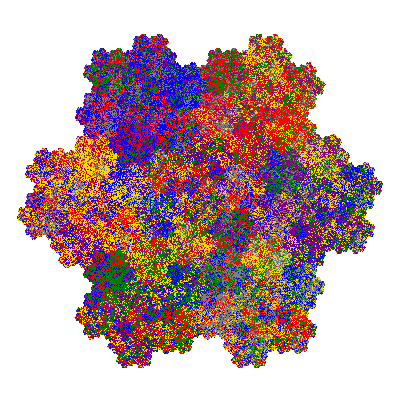
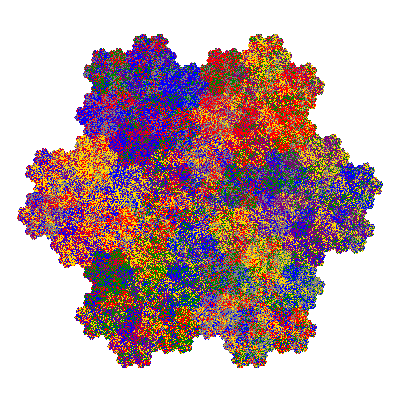
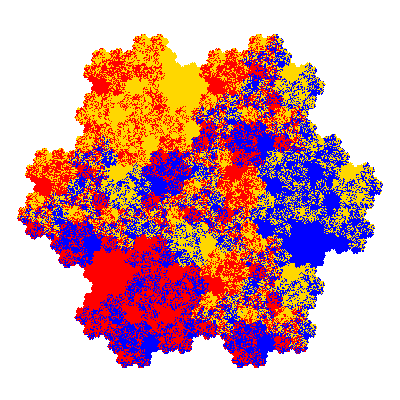
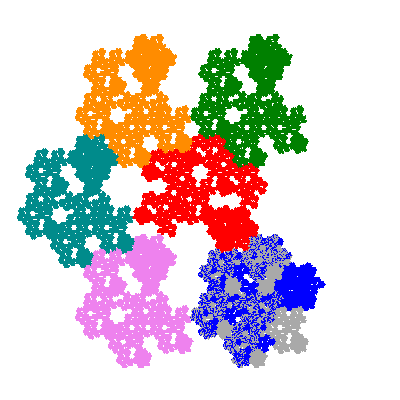
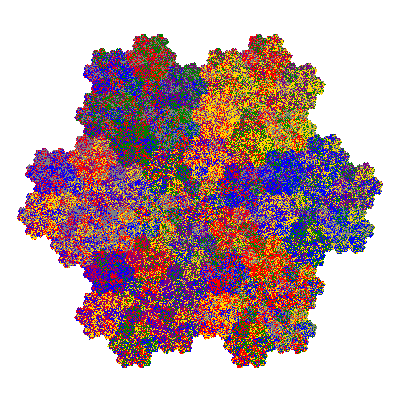
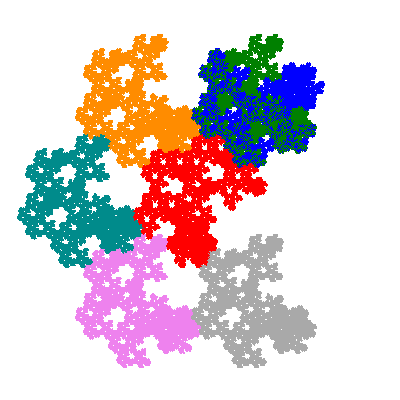
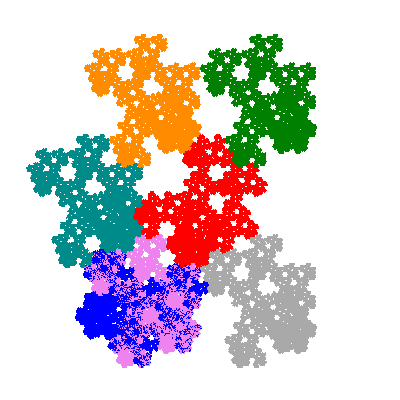
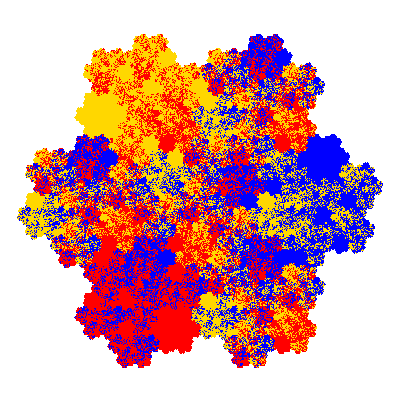
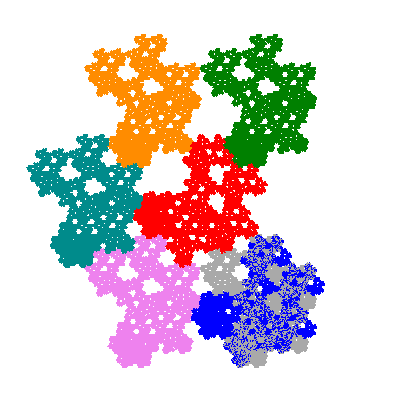
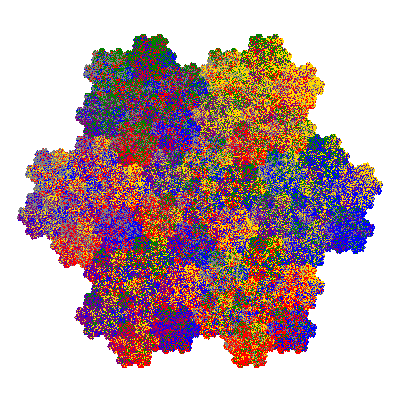
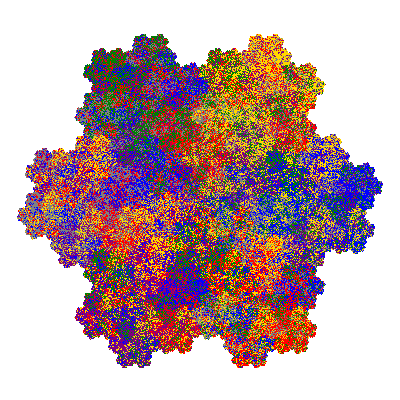
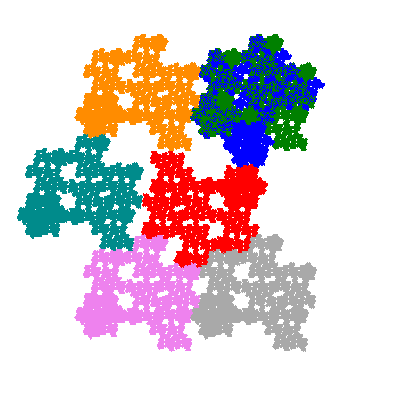
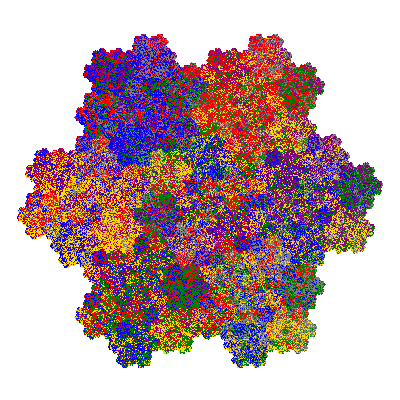
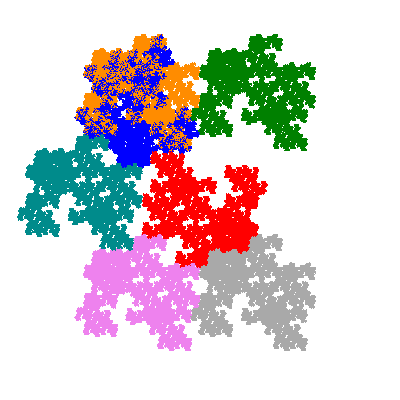
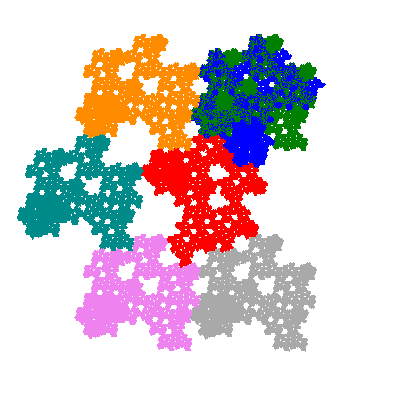
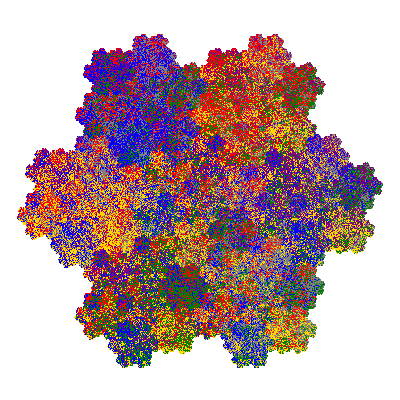
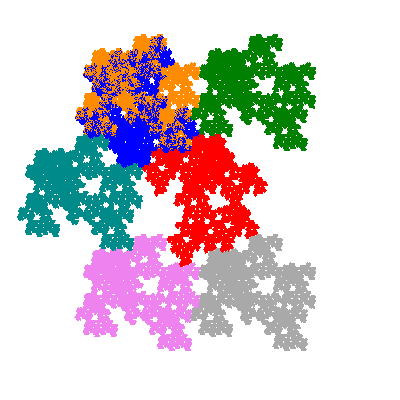
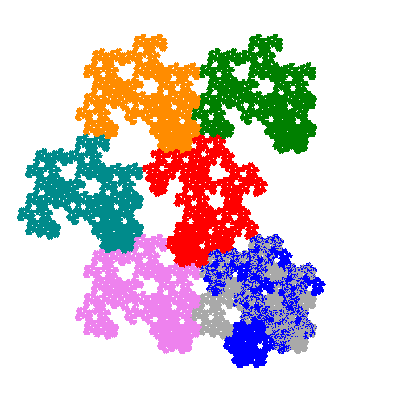
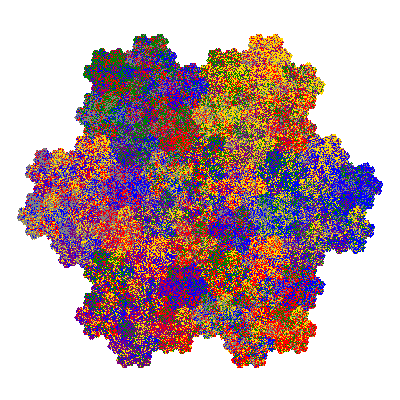
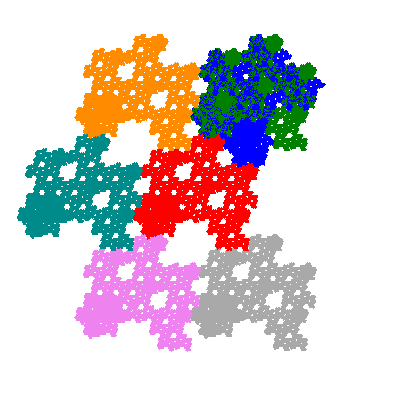
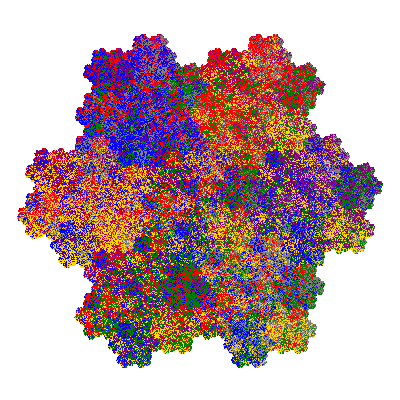
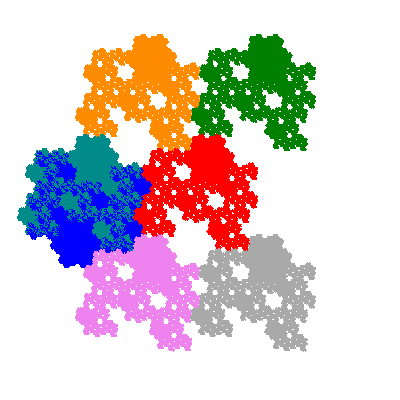
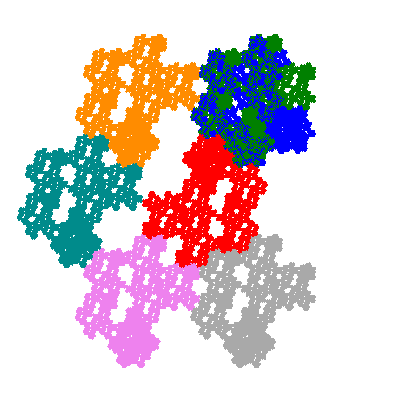
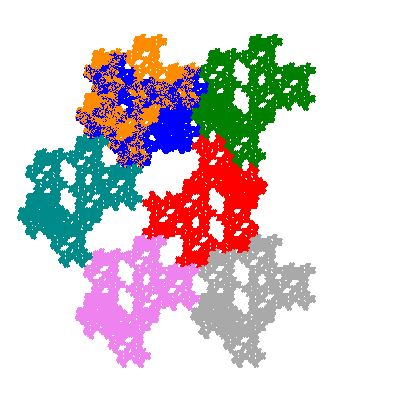
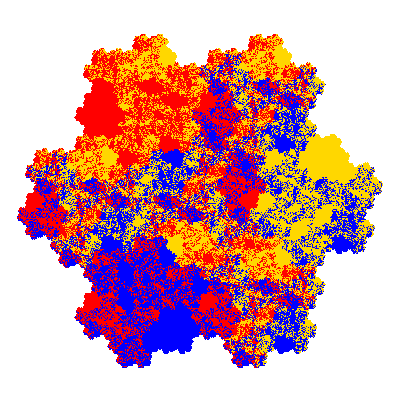
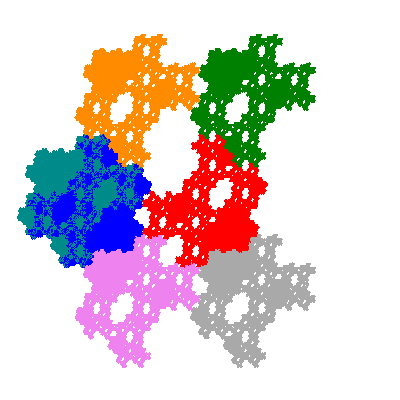
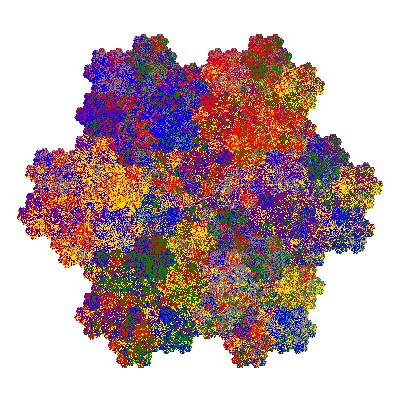
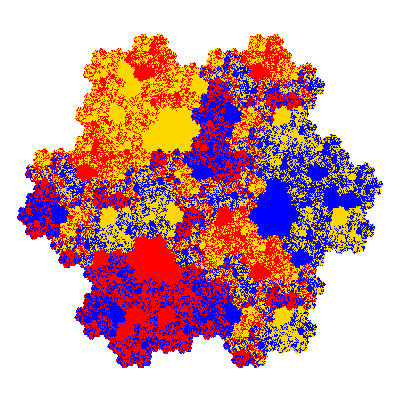
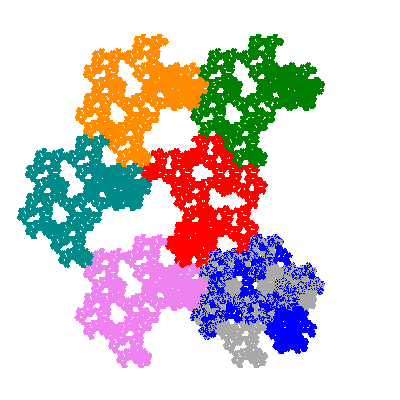
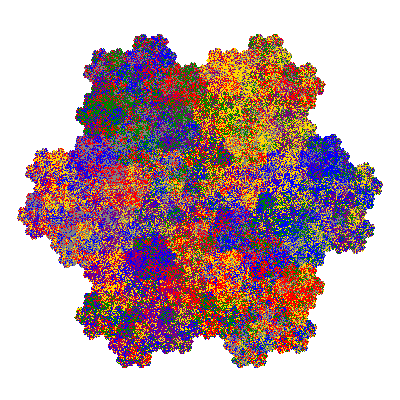
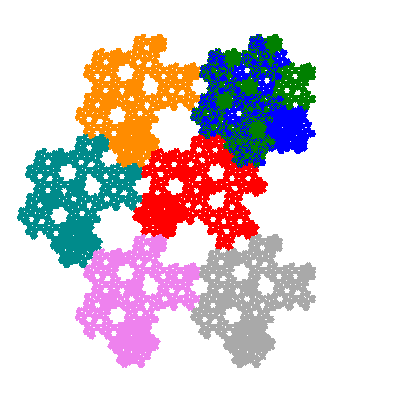
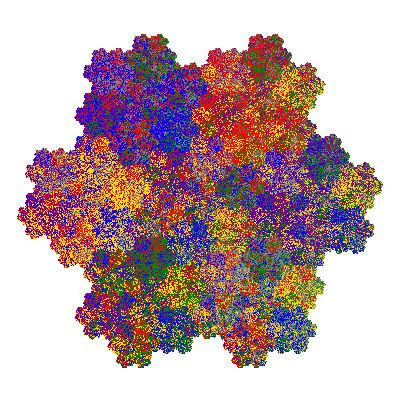
Pacmen rep-7-tiles are derivations of the flowsnake (Gosper curve) in which the 6 elements of the outer ring are packed into 5 of the 6 positions. The breaking of symmetry involved in this results in there being 11352 pacmen derived from each of the cis- and trans-flowsnakes, giving a total of 22704 pacmen rep-7-tiles.

As described in the overview of grouped element derivatives of the flowsnake there are 3 starting points, depending on which elements of the outer ring share an orientation. Unfortunately the sets of attractors obtained from each starting point overlap, so any enumeration of the attractors needs to take this into account.

Numbering the elements as shown

then for the first case

• element 1 can be moved to any of 5 positions
• element 0 can take any one of 6 orientations
• the elements of the outer ring (elements 1-6) can collectively take any one of 6 orientations
• elements 2-6 can be permuted (120 permutations)

giving a starting figure of 6*6*120*5 = 21,600 candidates. ( I considered permuting elements 1-6, but that is equivalent to the 2nd and 3rd points above.)

This can be reduced by a factor of two, as two elements at the same position with orientations a and b, or b and a, are the same IFS with the transforms in a different order, and therefore obviously produce the same attractor.

For the second case

• element 1 can be moved to positions 3 or 5
• element 0 can take take any of 6 orientations
• elements 1, 3 and 5 can take any of 6 orientations
• elements 2, 4 and 6 can take any of 6 orientations
• elements 2, 4 and 6 can be permuted
• elements 3 and 5 can be permuted

However

• when all of elements 1, 2, 3, 4, 5 and 6 have the same orientation this reduces to the first case
• the choice of permutation 246, 462 and 624, and of permutation 426, 264 and 642, is equivalent to a different choice of orientation for the triplet.
• the choice of permutation 35 and 53, is equivalent to a different choice of orientation for the triplet 135.

Hence the number of candidates arising is 720. Of these 288 (where the difference between the orientations of the two sets of 3 is even) duplicate candidates arising from the 1st case, so this adds 432 tiles.

For the third case

• element 1 is moved to position 4 only
• element 0 can take take any of 6 orientations
• elements 1 and 4 can take any of 6 orientations
• elements 2 and 5 can take any of 6 orientations
• elements 3 and 6 can take any of 6 orientations
• elements 2 and 4 can be permuted
• elements 3 and 5 can be permuted

However

• permutation of elements 2 and 4, or elements 3 and 5, is equivalent to a different choice of orientation for the pair
• the orientation of elements 1 and 4 has no effect on the attractor because the combination of the two elements is always the same shape
• when all of elements 2, 3, 5 and 6 have the same orientation this reduces to the first case

Hence the number of candidates resulting is 180. Of these 60 duplicate candidates arising from the 1st case, so this adds 120 tiles.

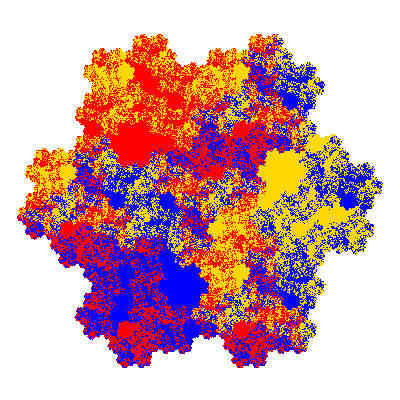
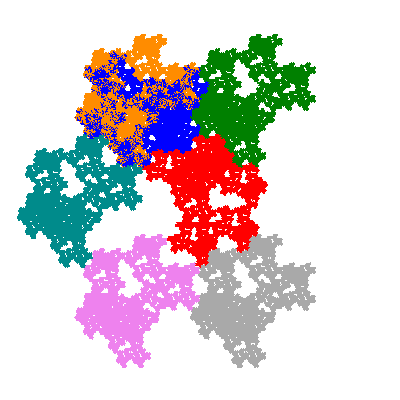
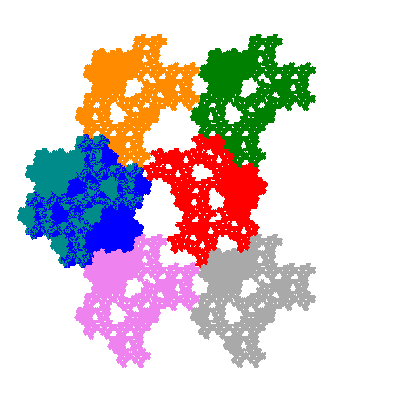
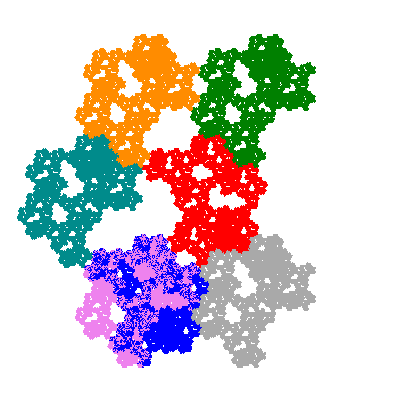
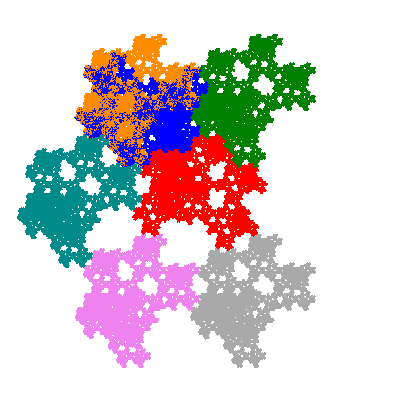
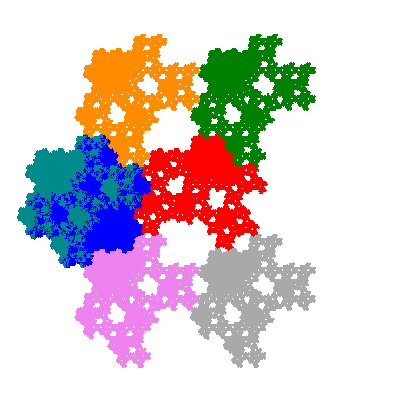
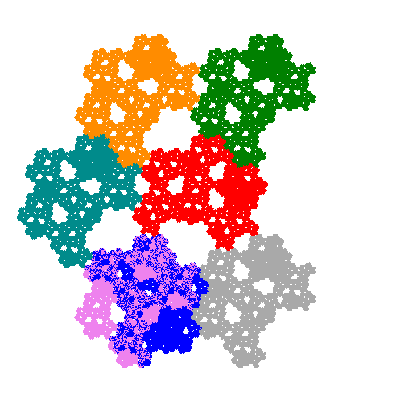
Each pacman occupies one half, one third, or one sixth of the parent flowsnake, and therefore tiles the plane with 2, 3 or 6 copies in the unit cell. All tiles resulting from the second case have 3 elements in the unit cell, and all tiles resulting from the third case have 2 elements in the unit cell.

More generally, if elements 2 and 5, and elements 3 and 6, after permutation, have the same orientation, and element 1 is moved to position 4 then the tiles has two copies in the unit cell.

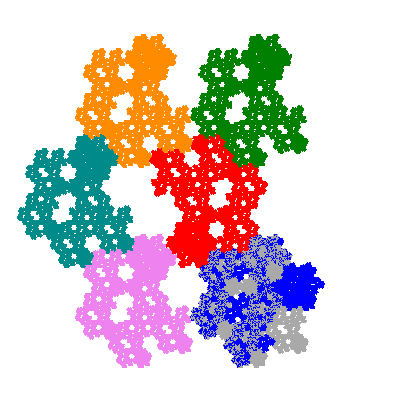
If all elements moved are moved 2 or 4 positions (rotated by 120° or 240°) the pacman occupies a third of the parent flowsnake. I haven't confirmed the conjecture that otherwise the pacman occupies a sixth of the parent flowsnake.

• derivatives of cis-flowsnake, with 2 copies in the unit cell (position signature 11211)
• derivatives of trans-flowsnake, with 2 copies in the unit cell (position signature 11211)

The directly similar pacmen, where 5 elements of the outer ring are fixed, start here.

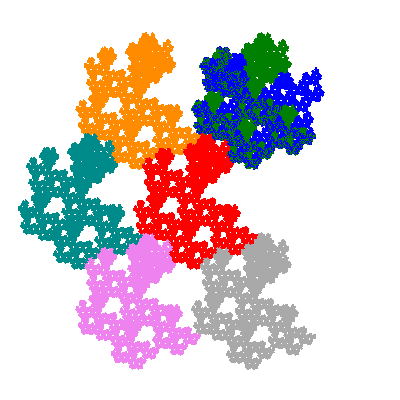
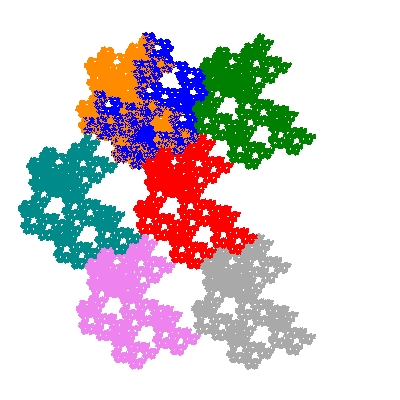
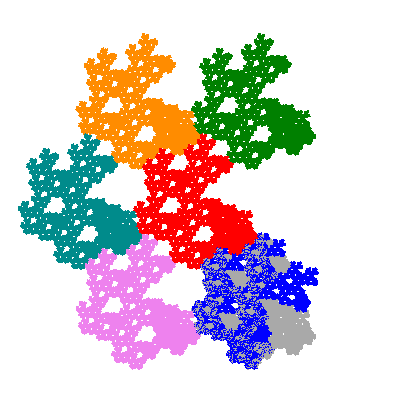
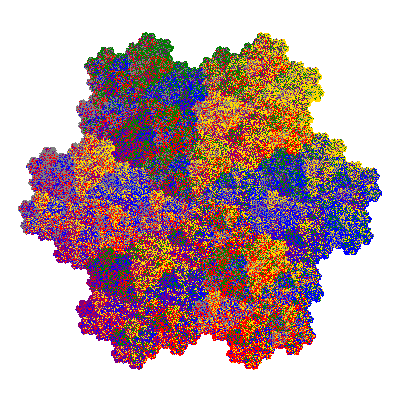
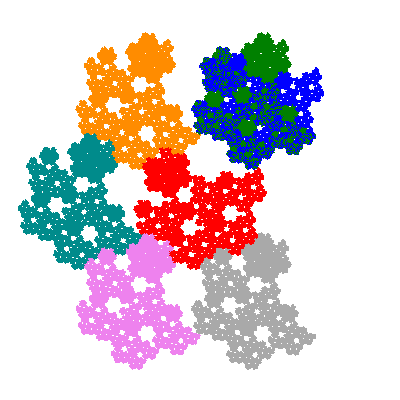
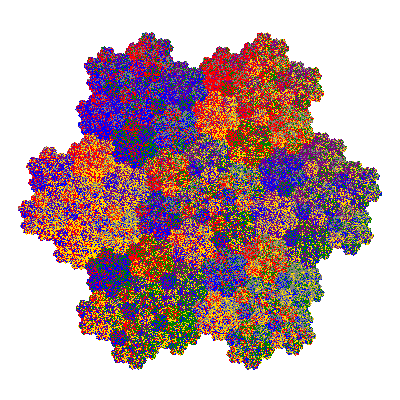
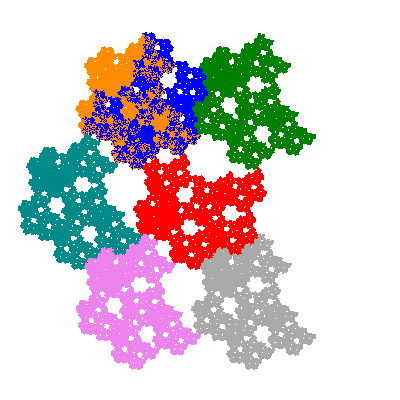
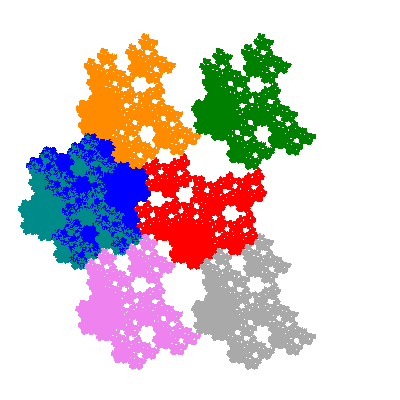
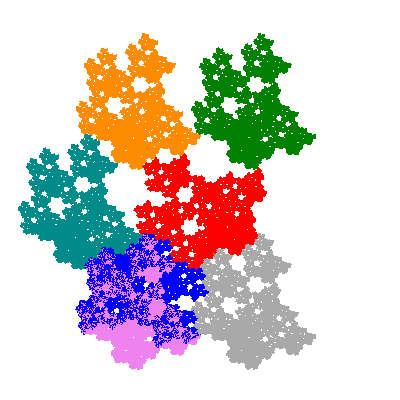
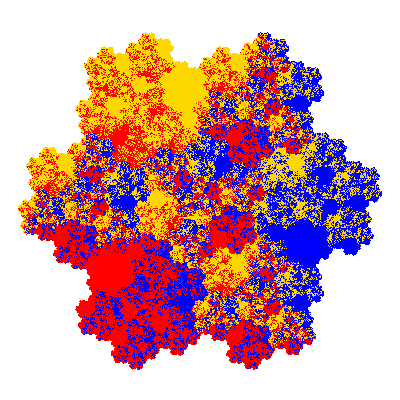
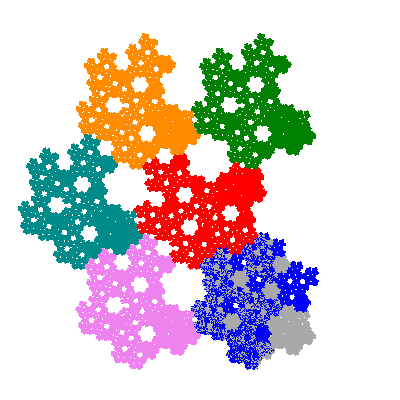
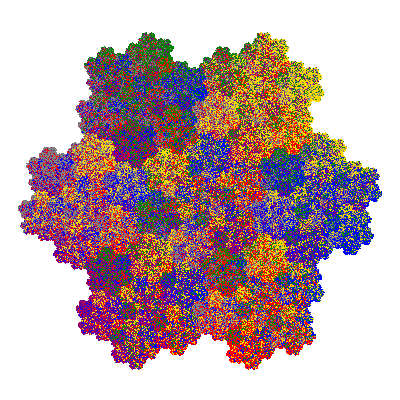
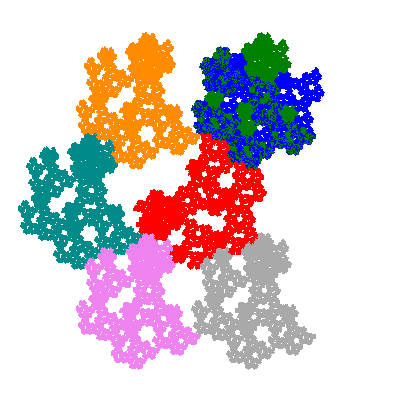
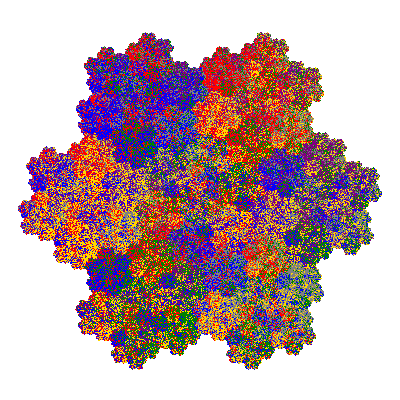
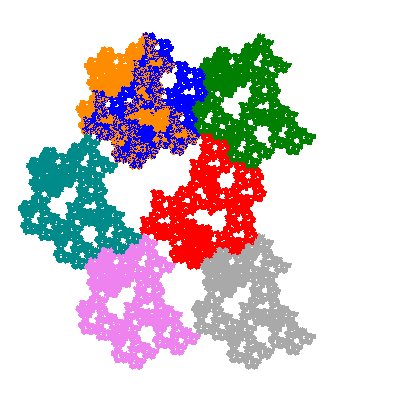
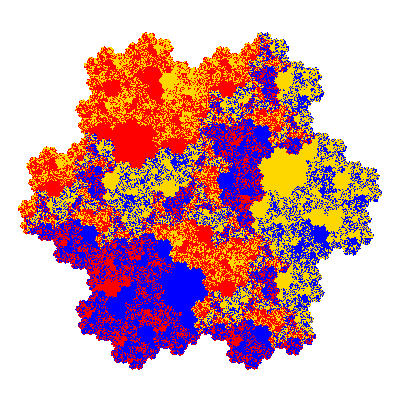
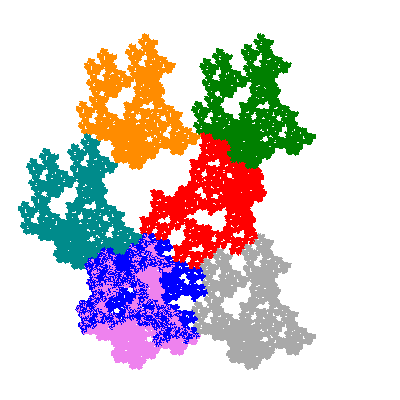
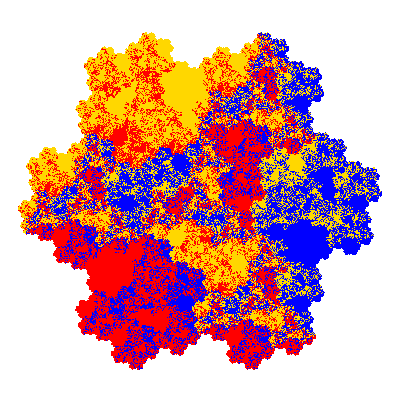
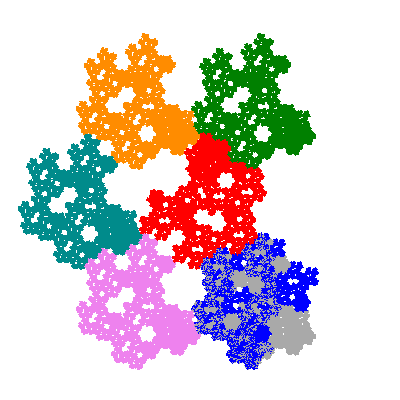
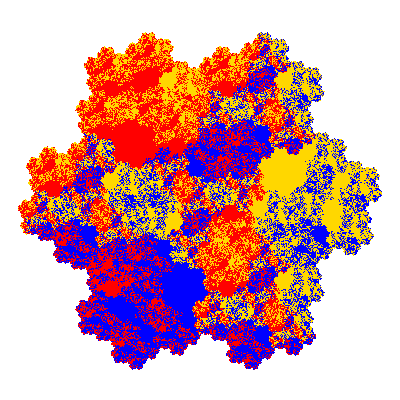
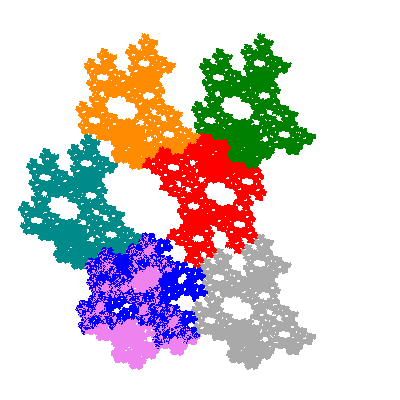
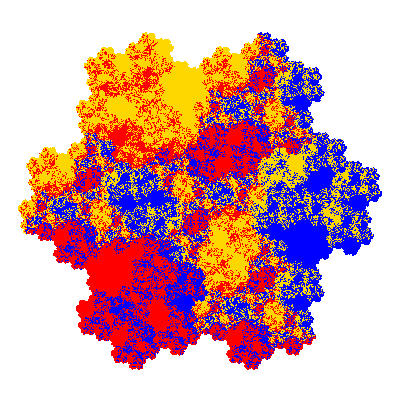
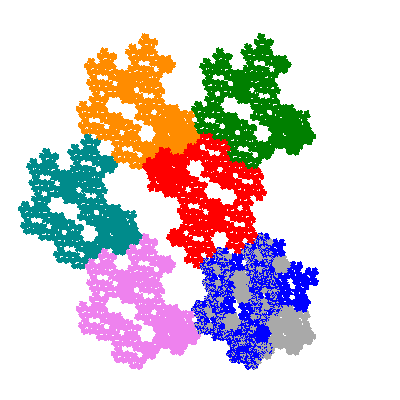
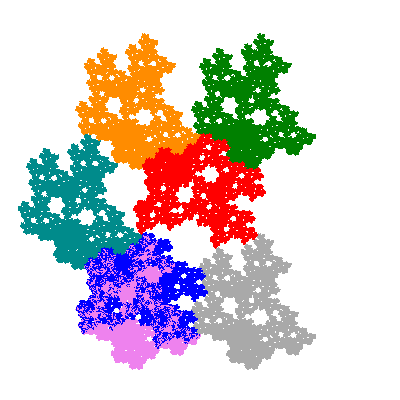
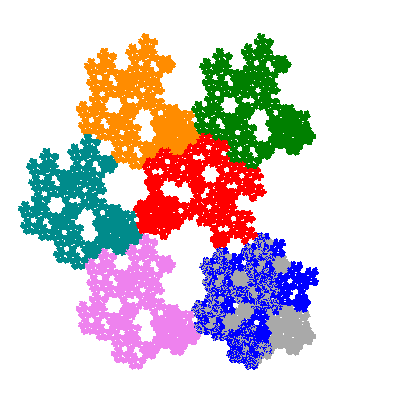
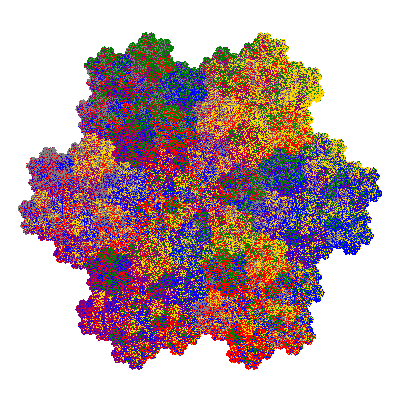
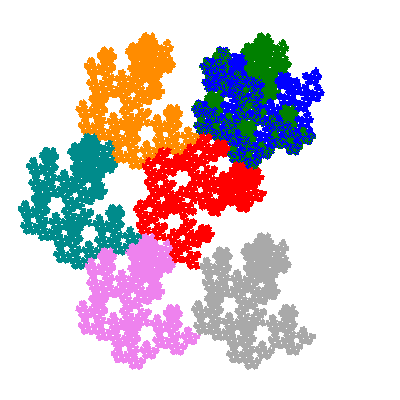
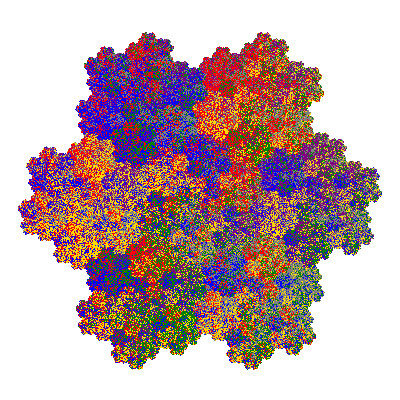
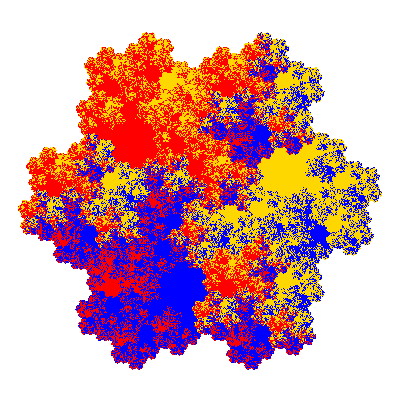
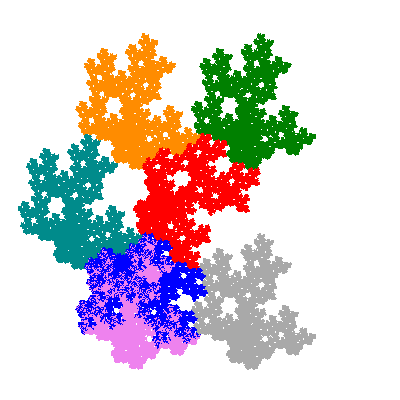
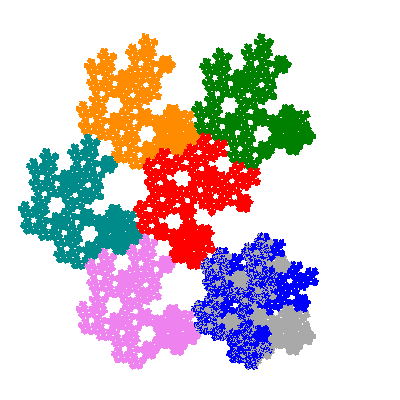
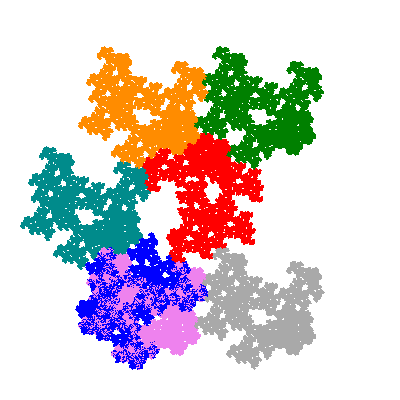
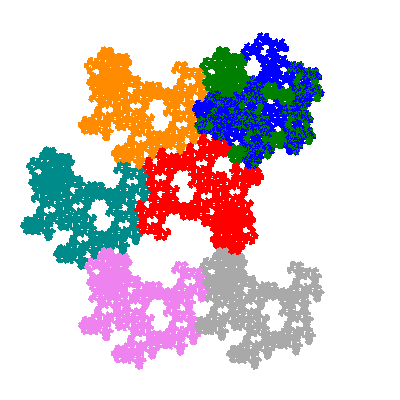
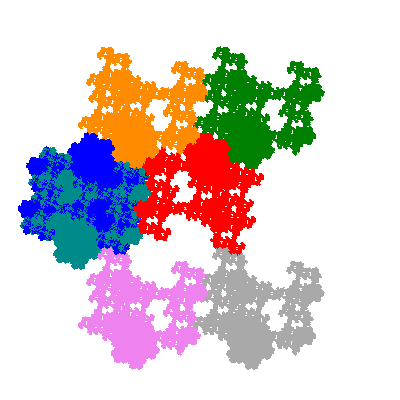
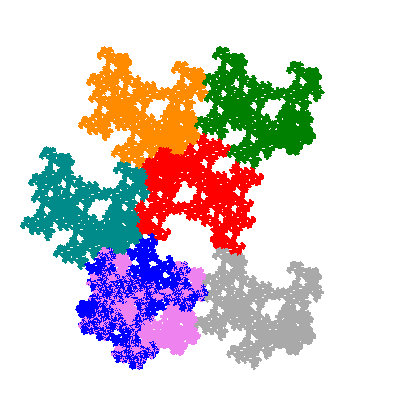
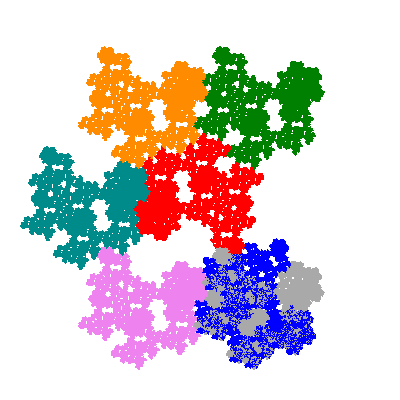
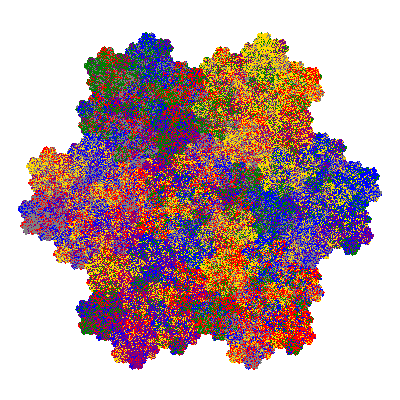
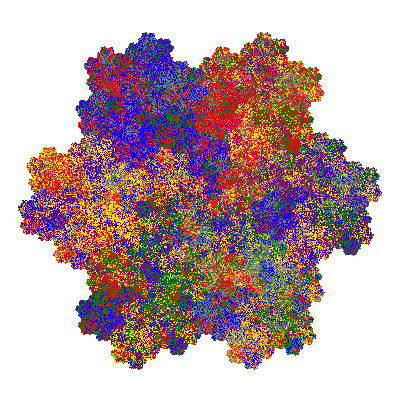
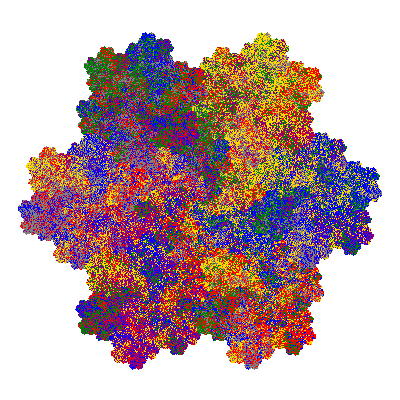
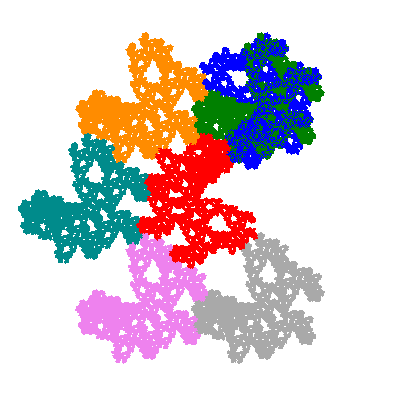
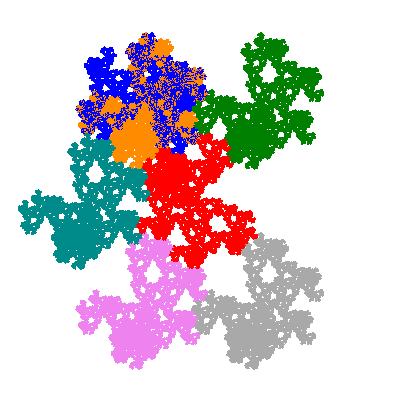
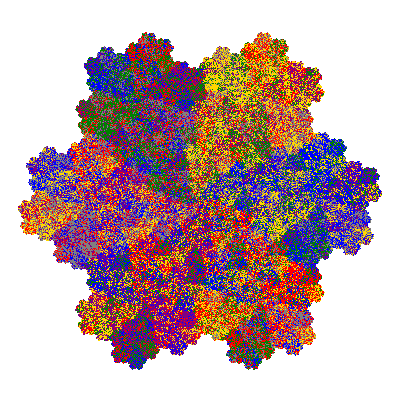
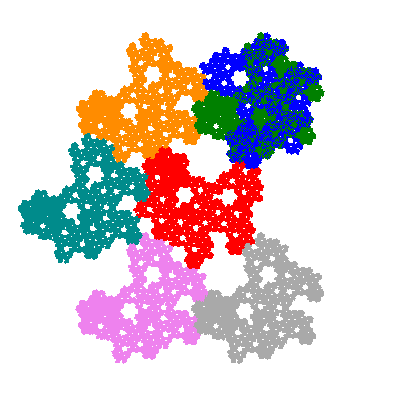
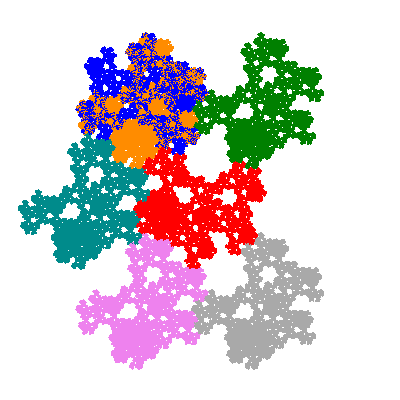
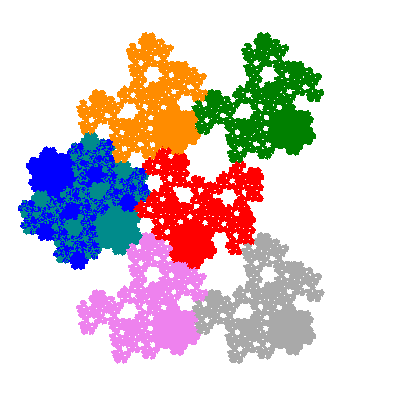
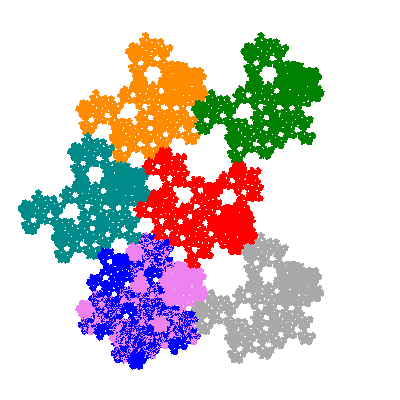
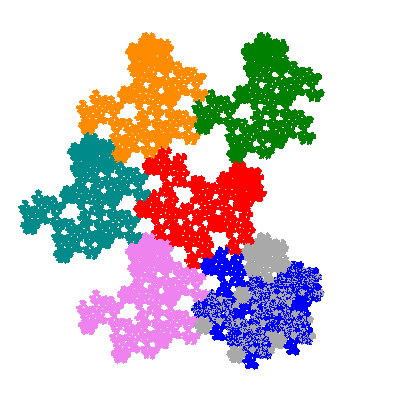
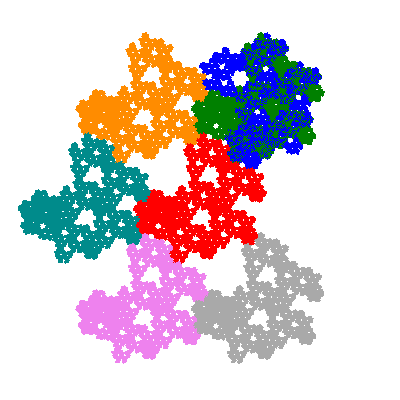
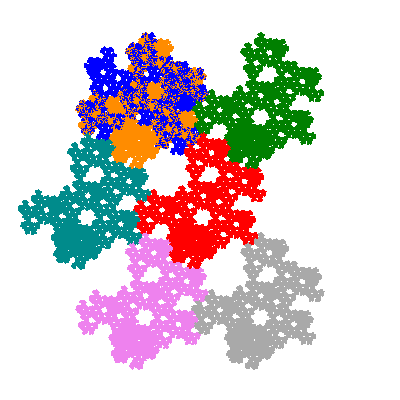
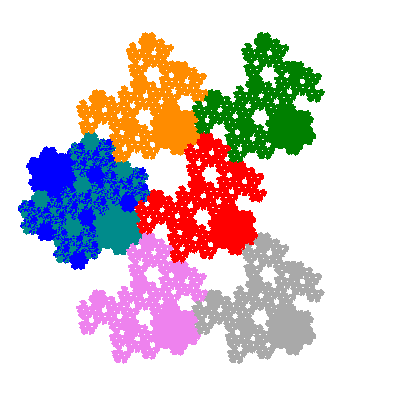
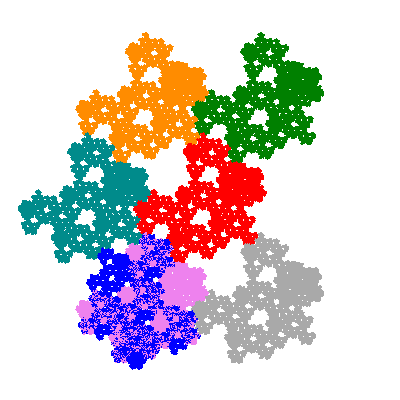
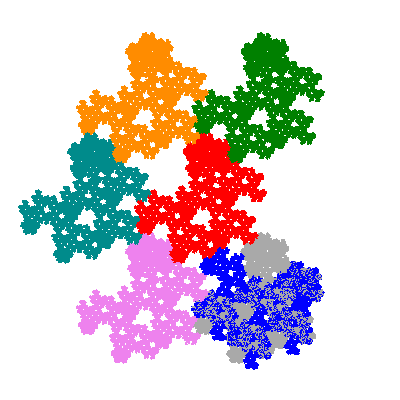
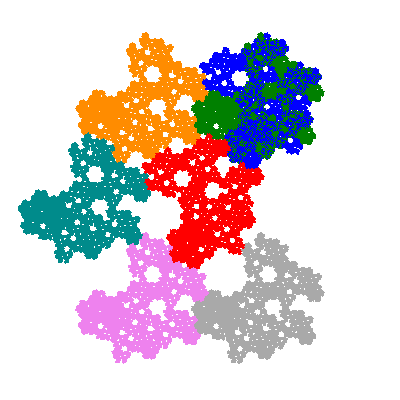
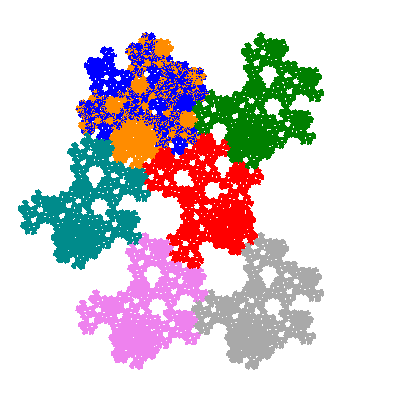
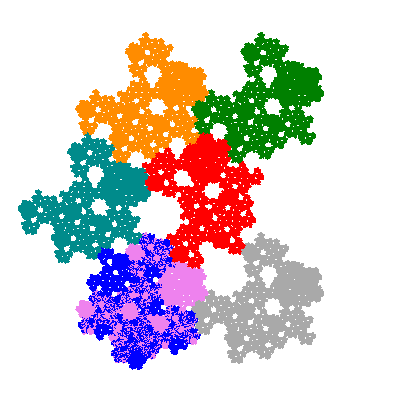
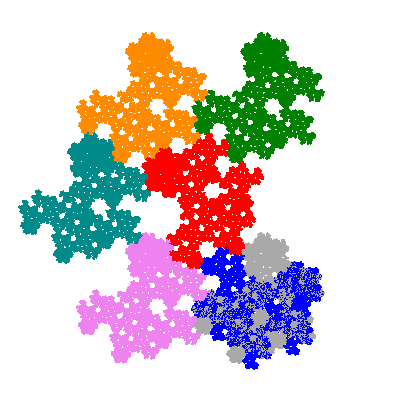
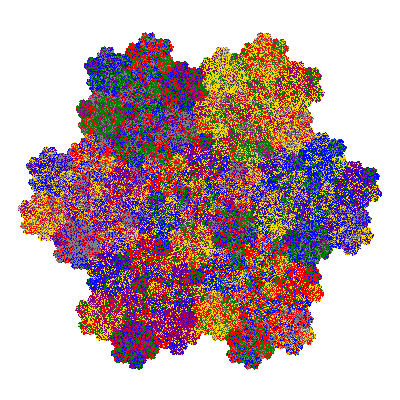
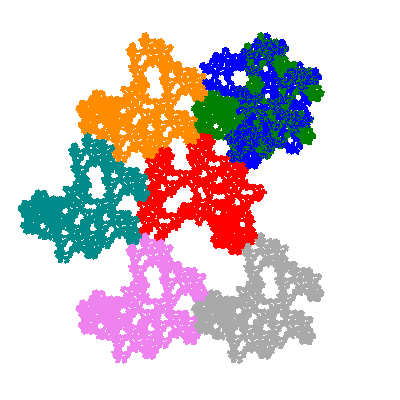
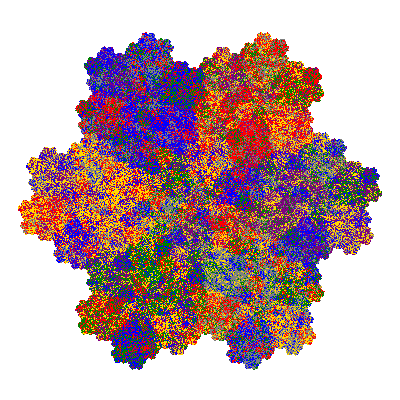
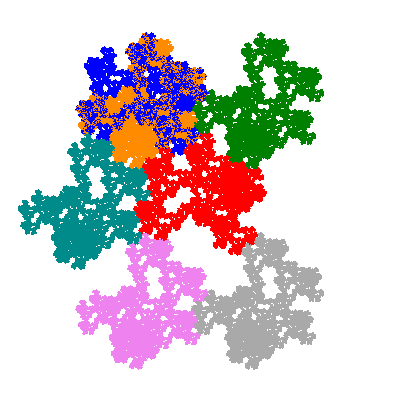
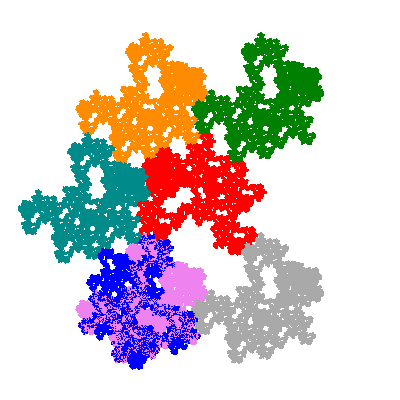
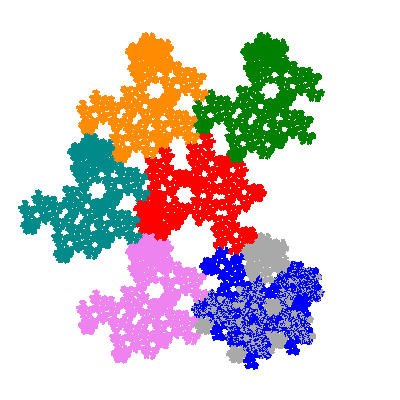
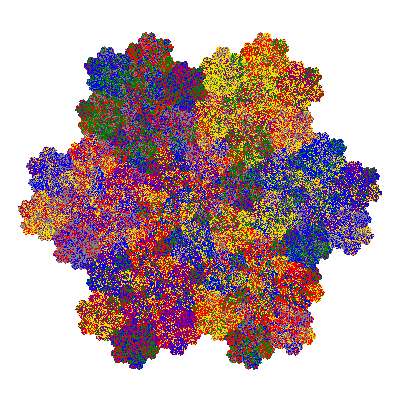
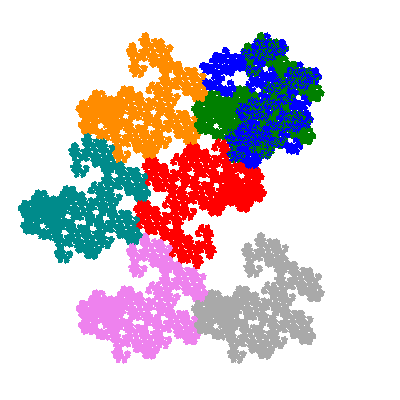
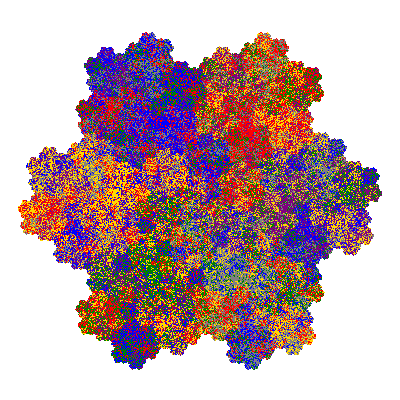
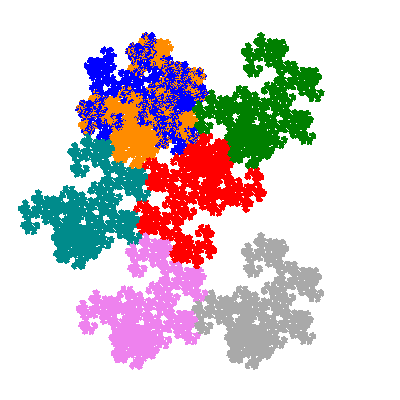
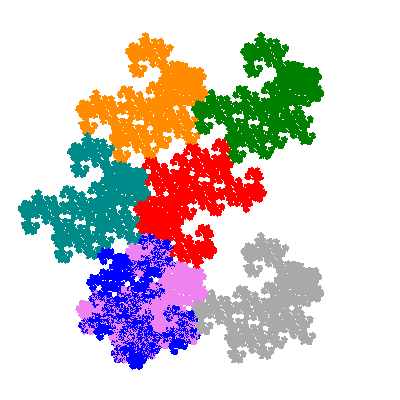
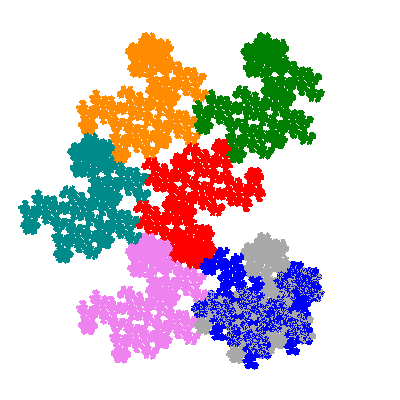
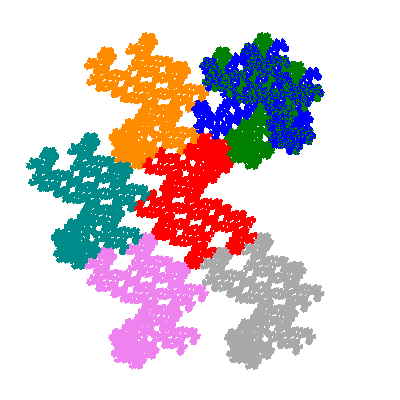
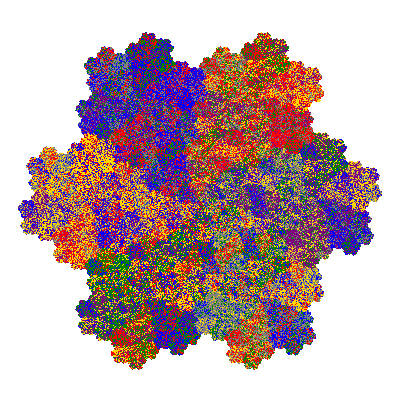
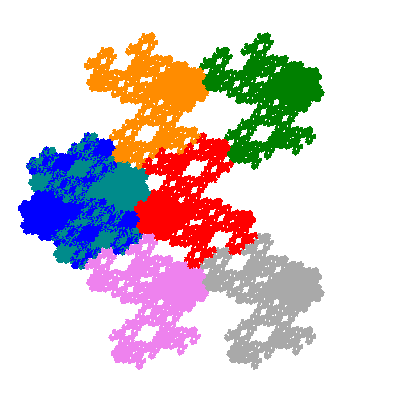
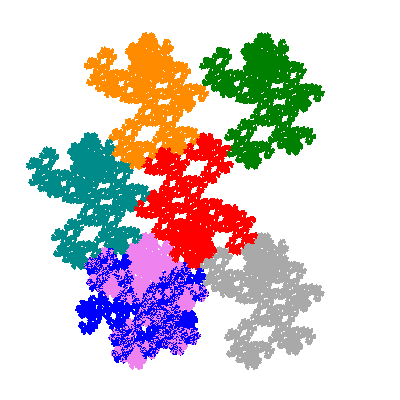
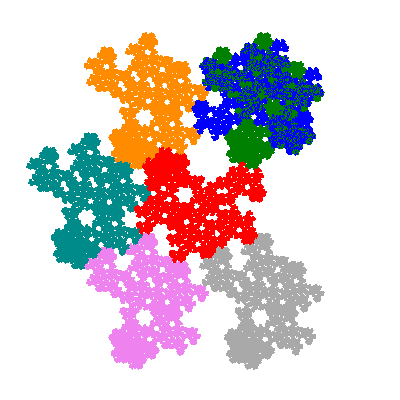
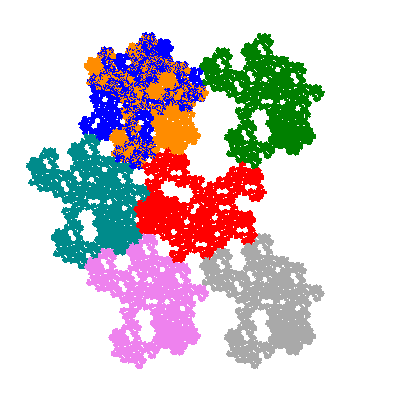
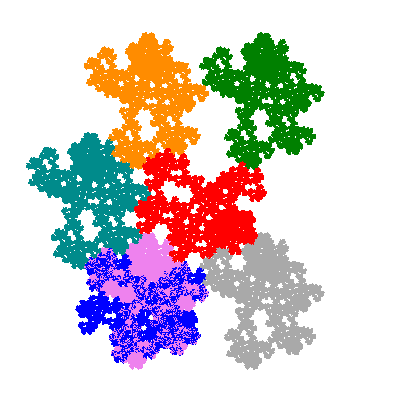
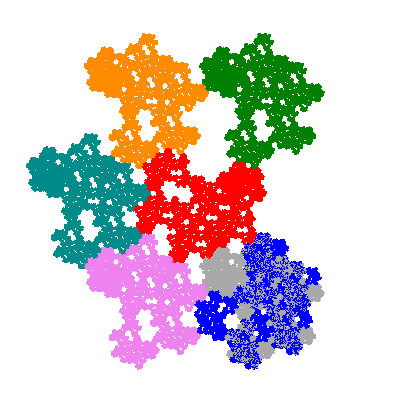
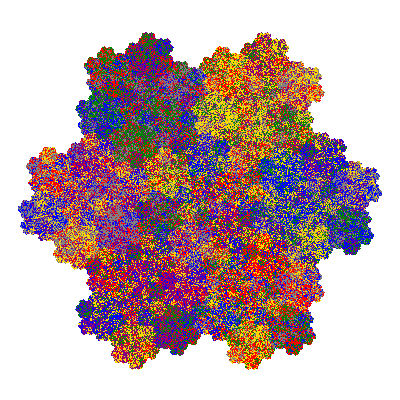
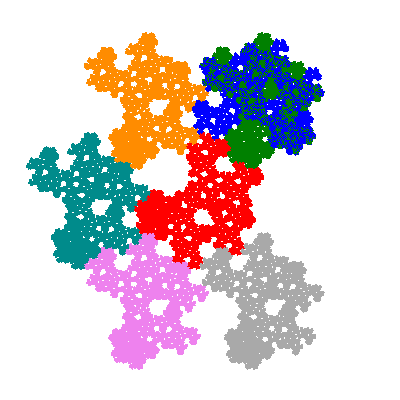
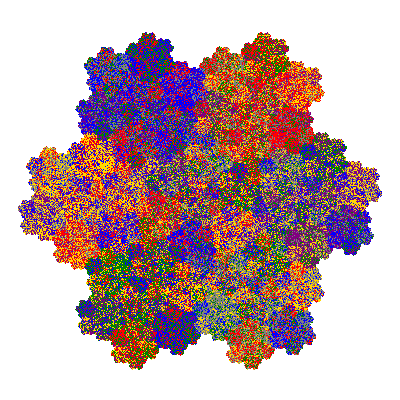
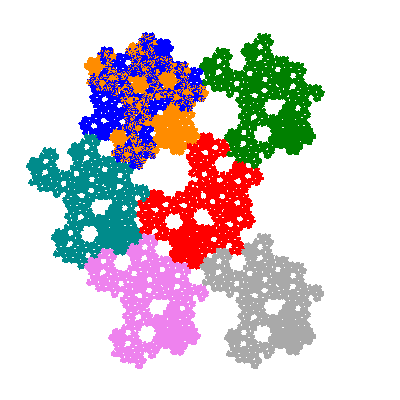
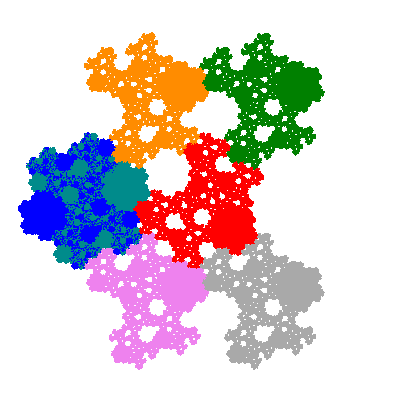
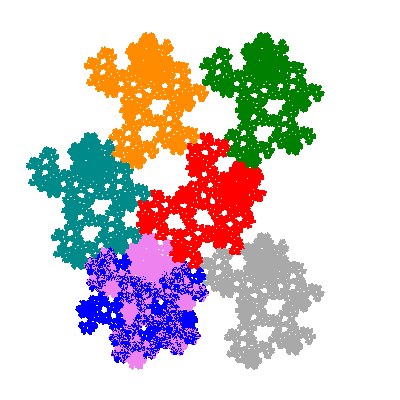
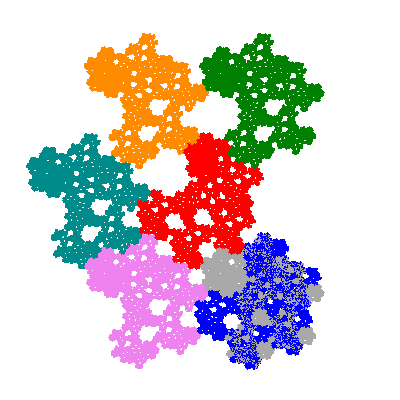
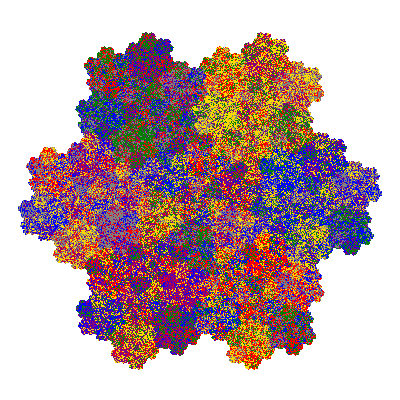
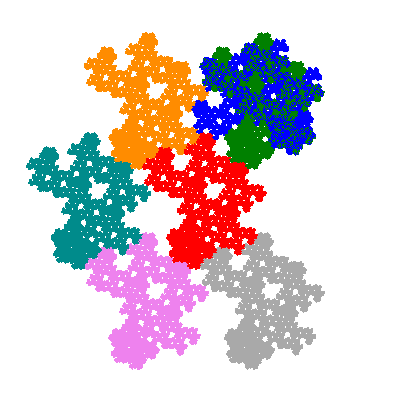
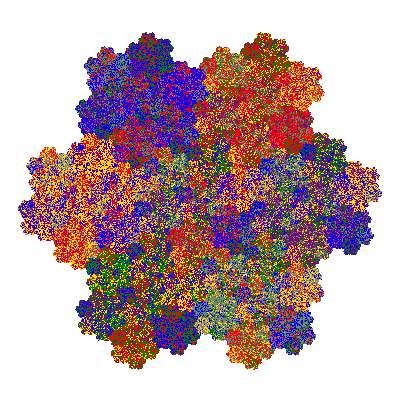
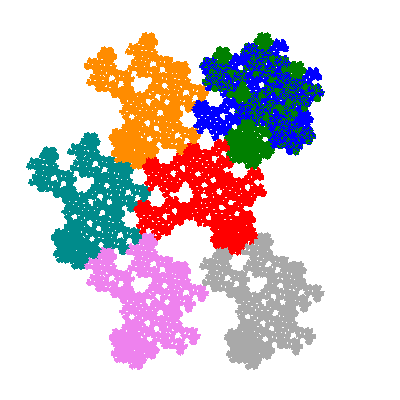
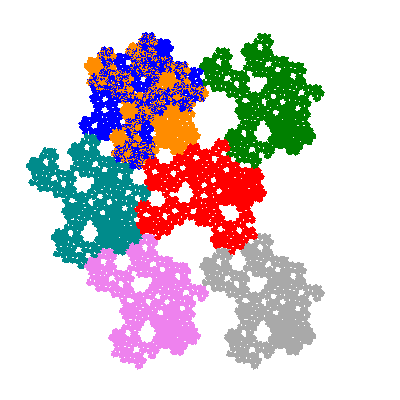
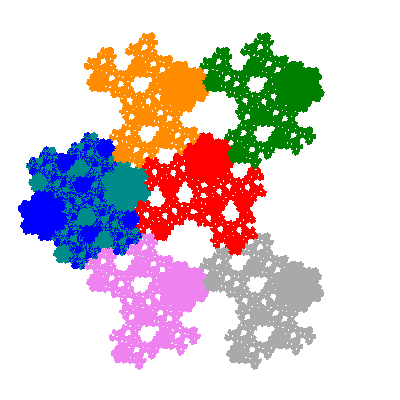
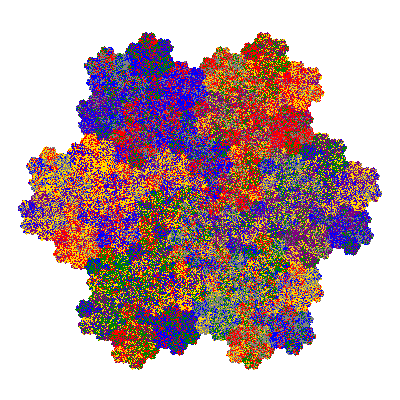
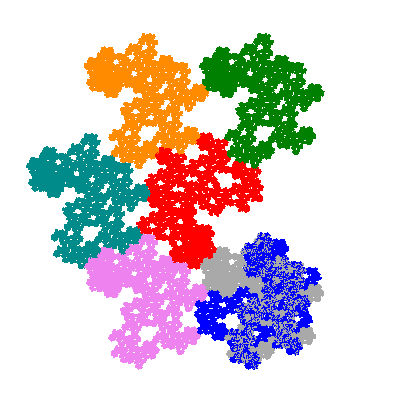
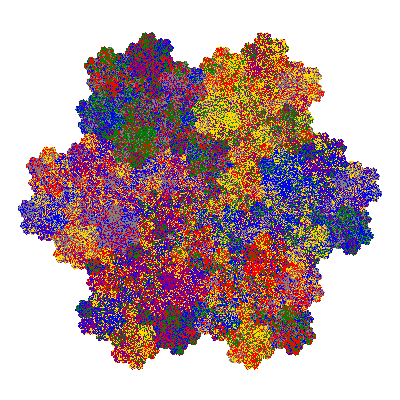
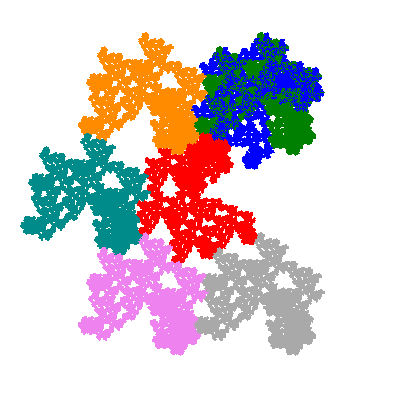
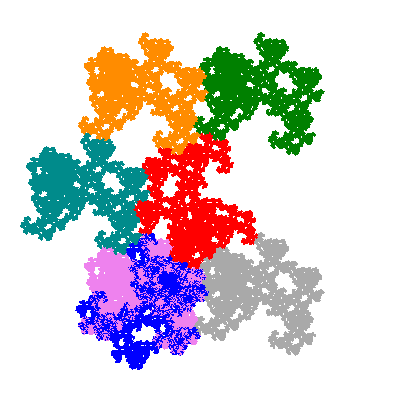
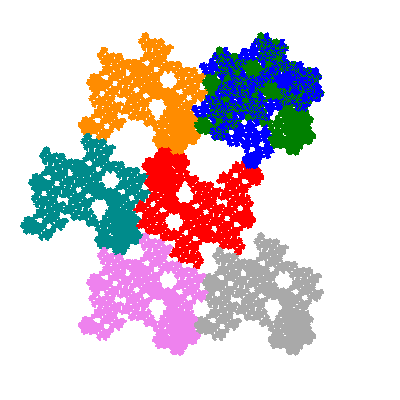
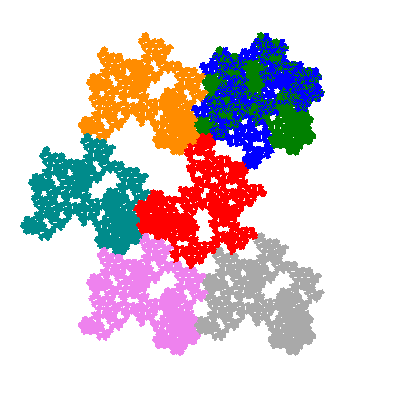
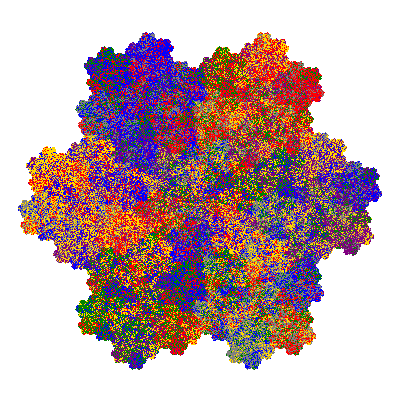
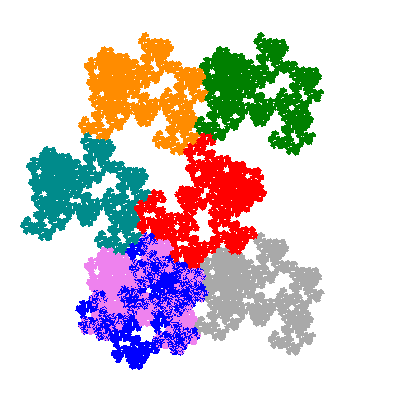
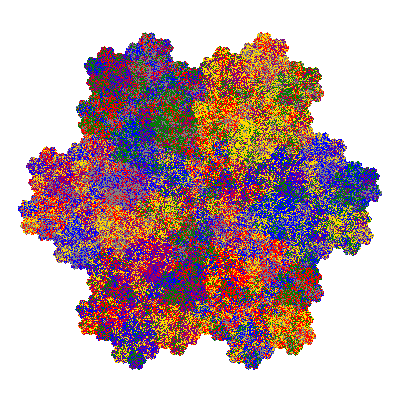
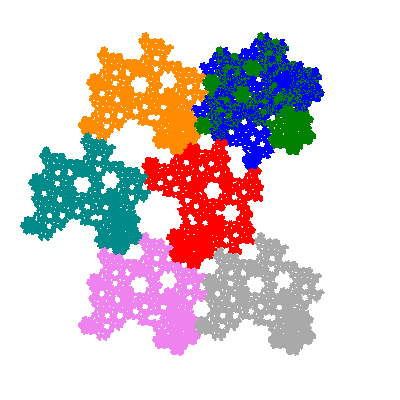
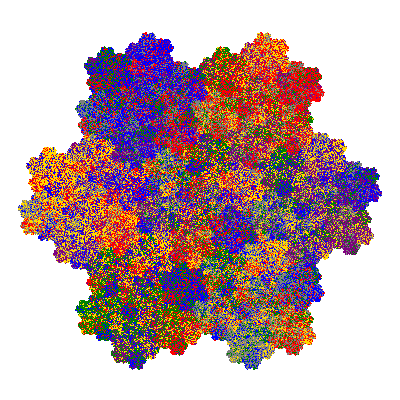
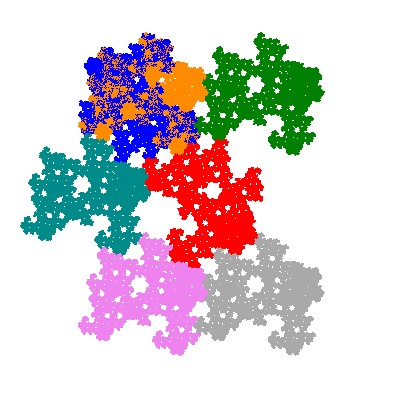
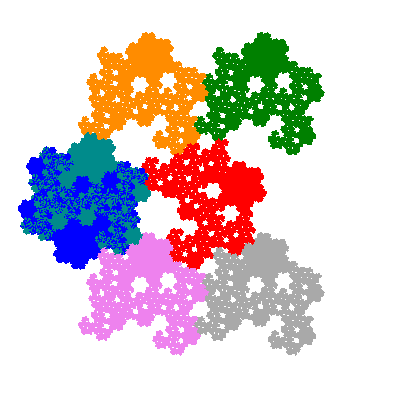
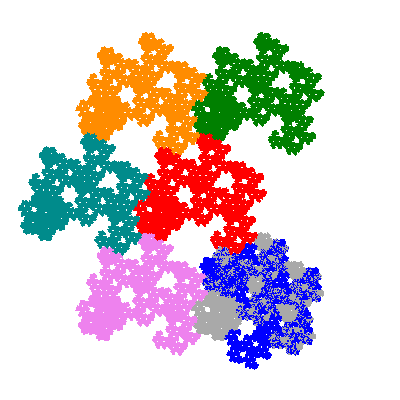
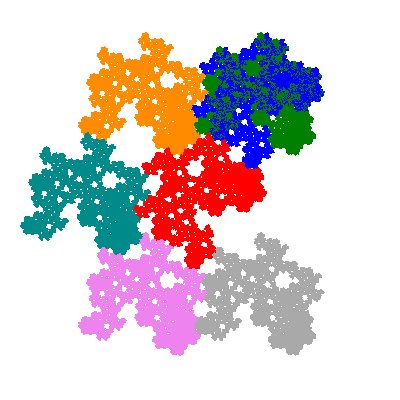
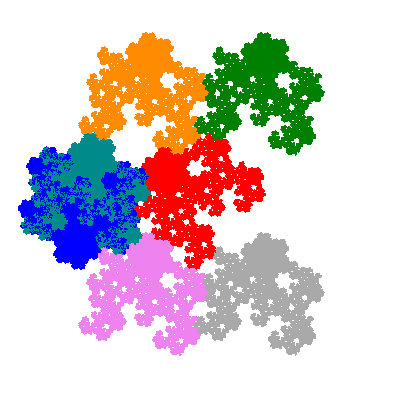
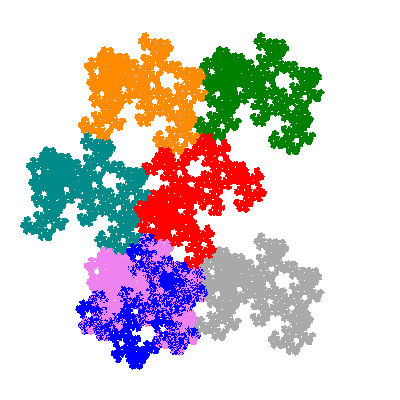
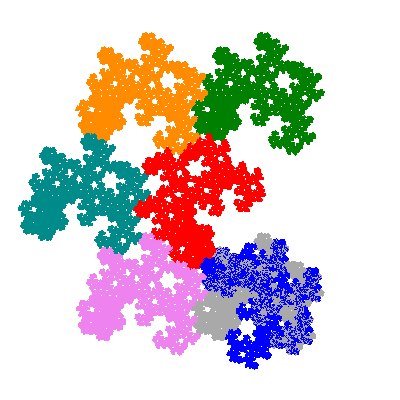
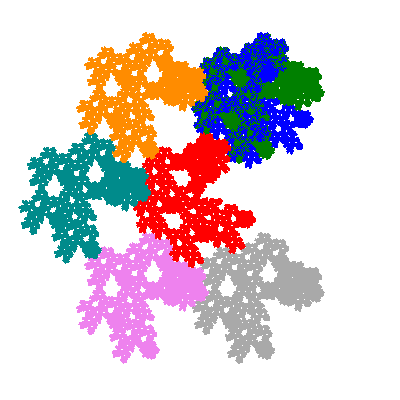
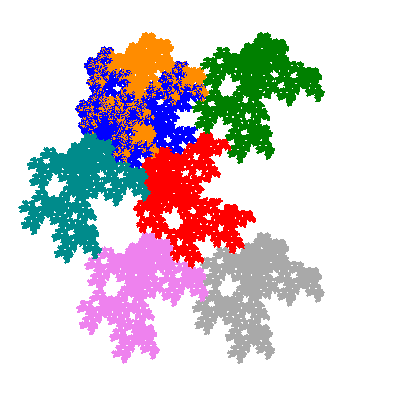
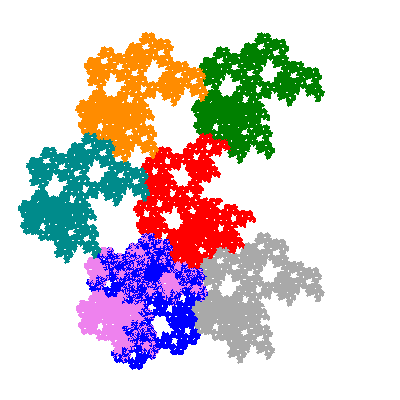
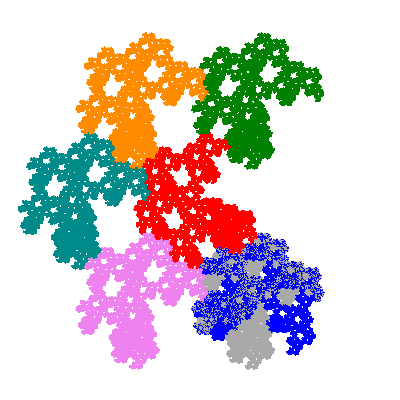
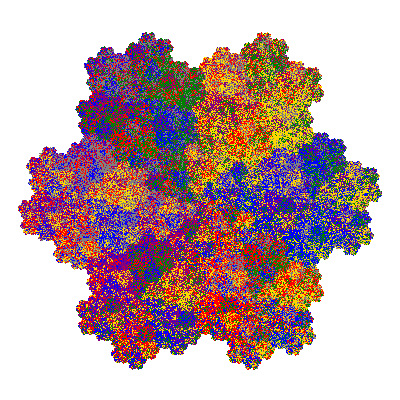
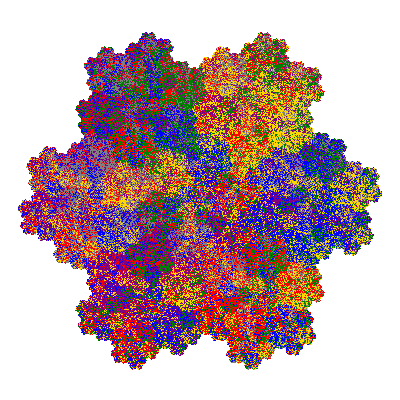
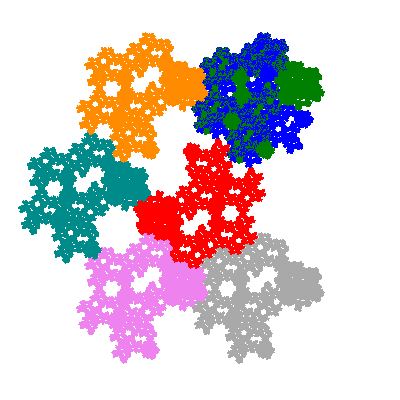
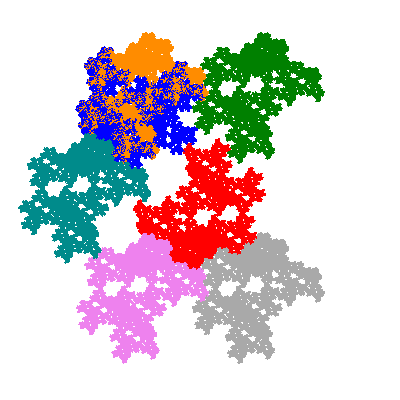
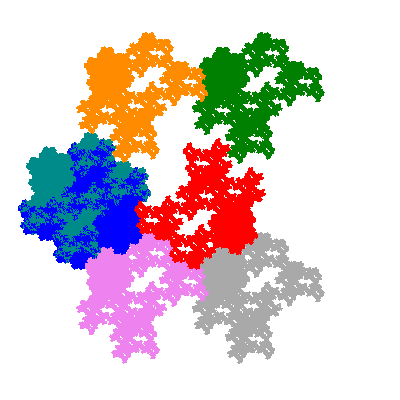
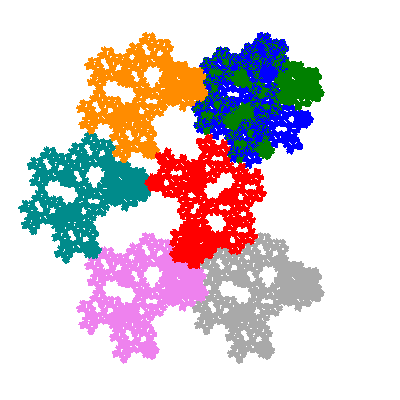
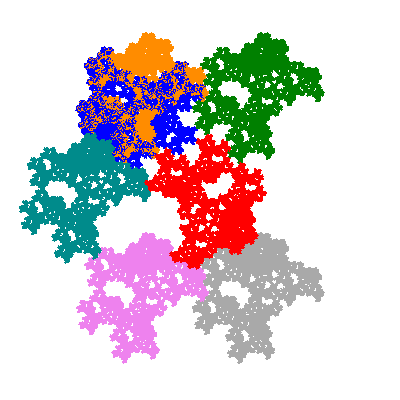
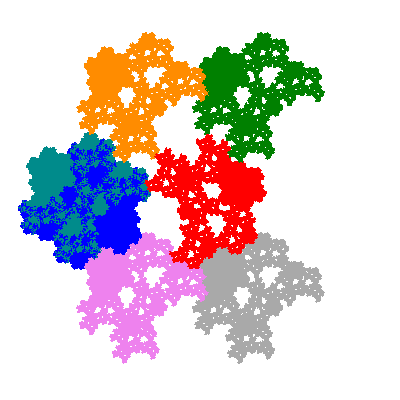
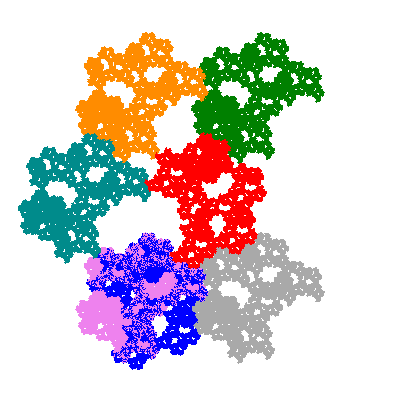
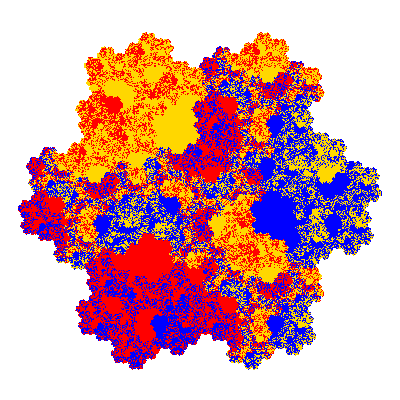
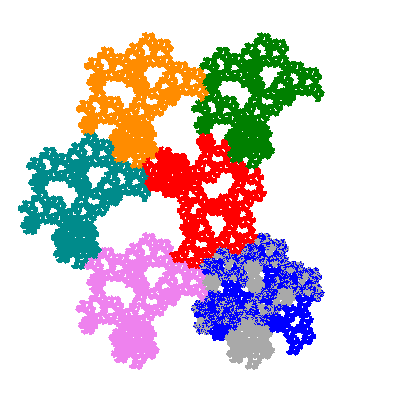
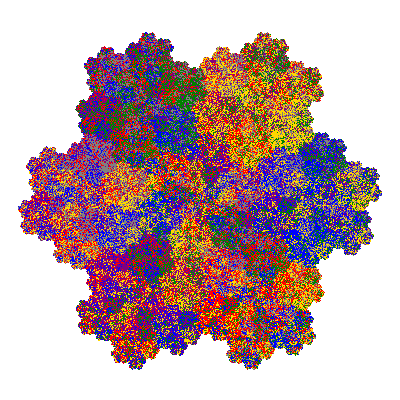
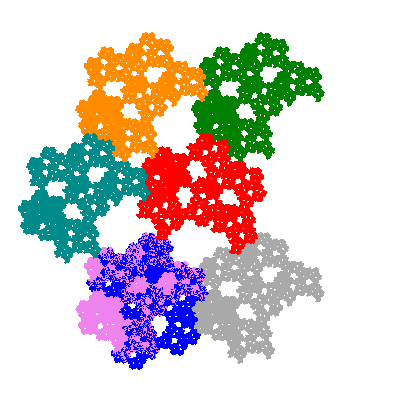
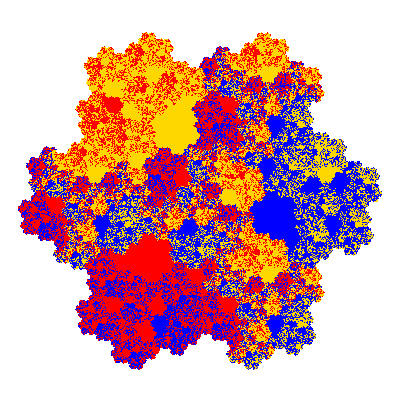
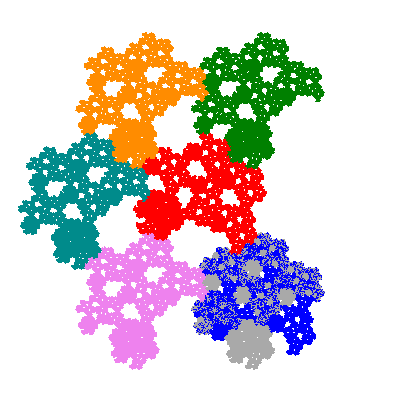
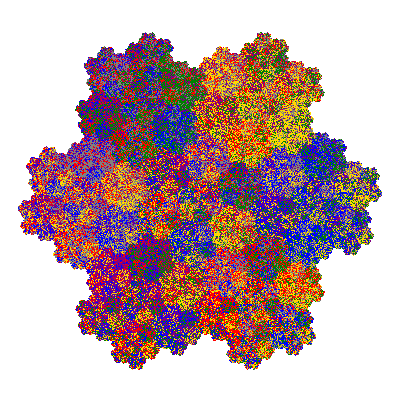
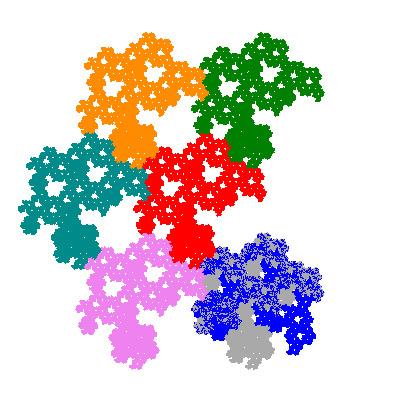
The inversely similar pacmen, where 5 elements of the outer ring are fixed, start here.

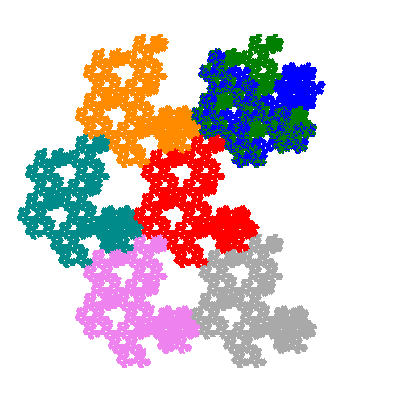
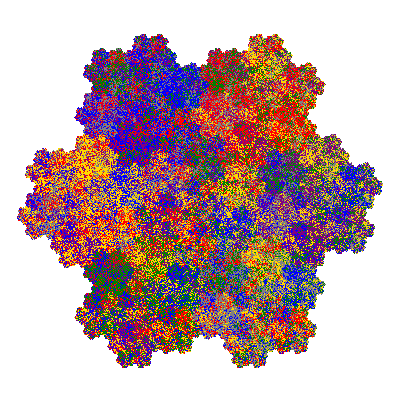
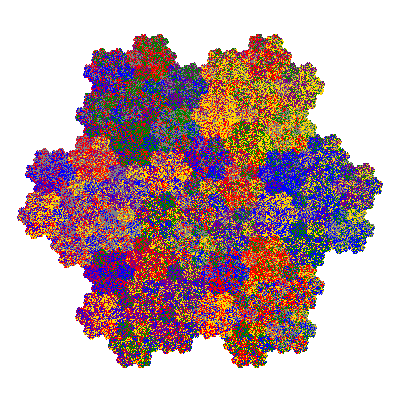
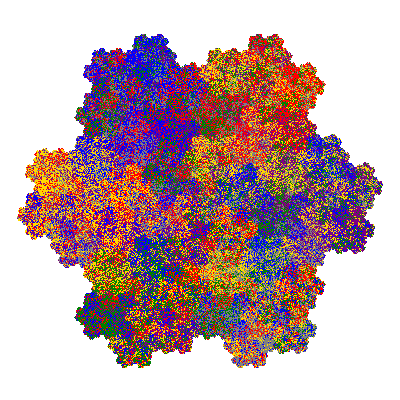
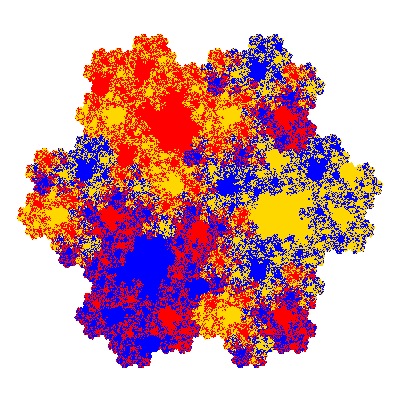
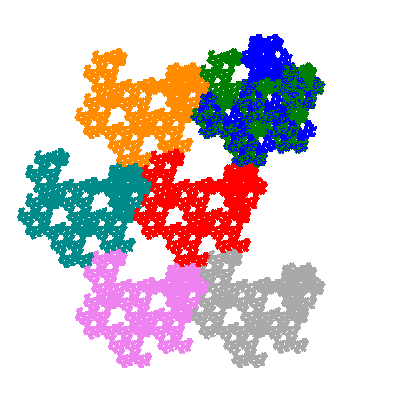
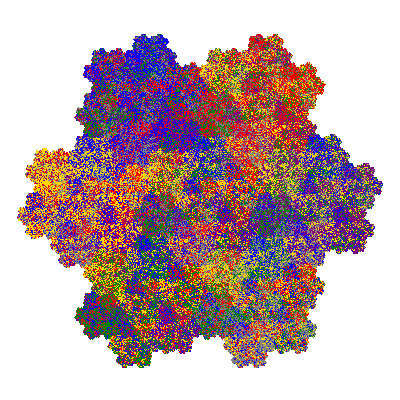
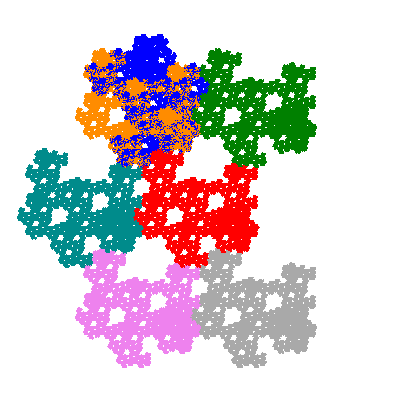
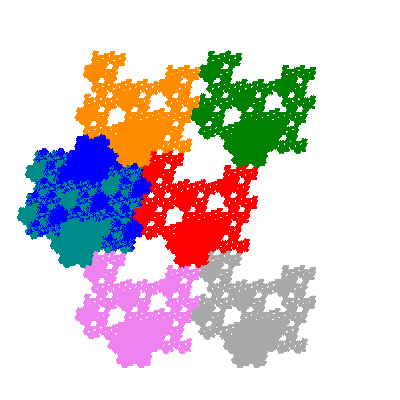
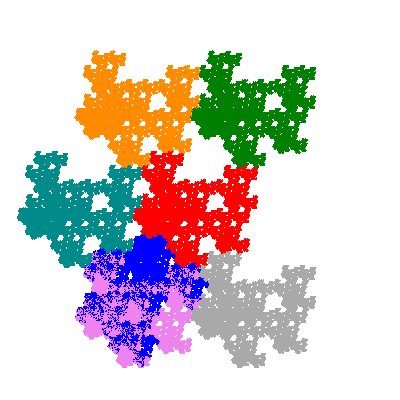
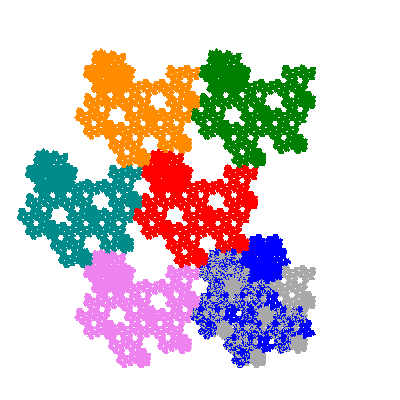
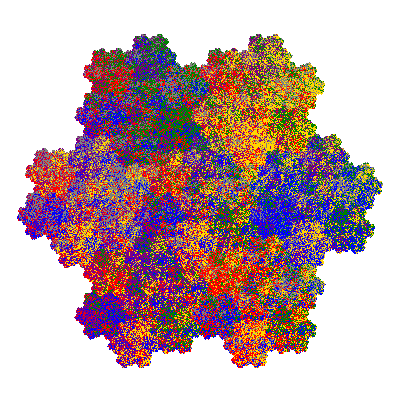
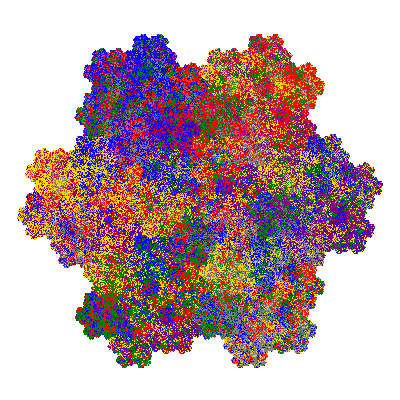
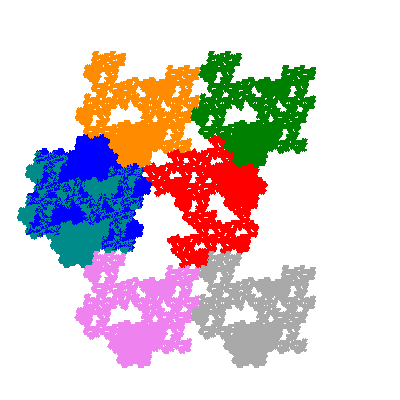
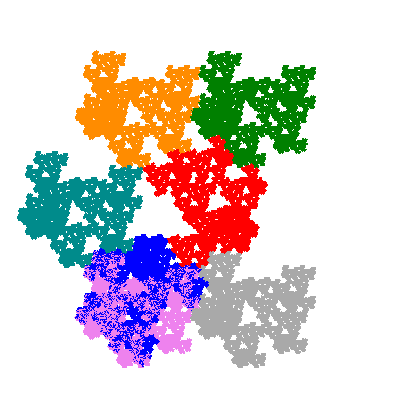
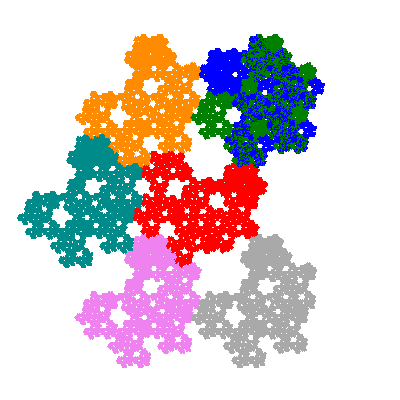
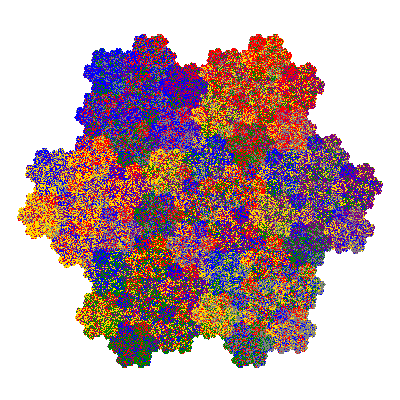
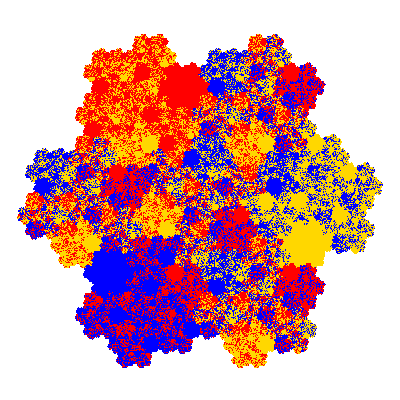
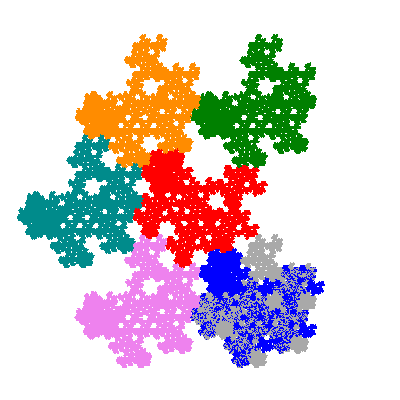
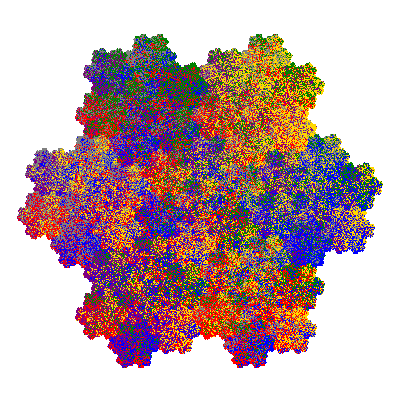
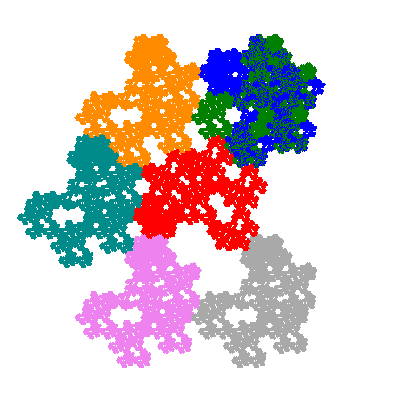
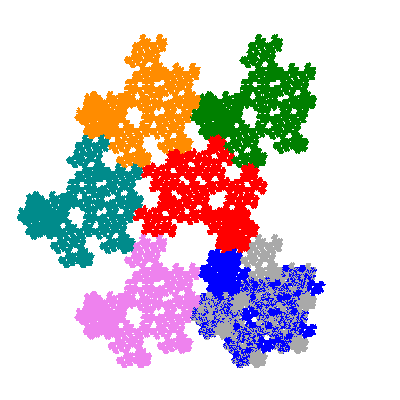
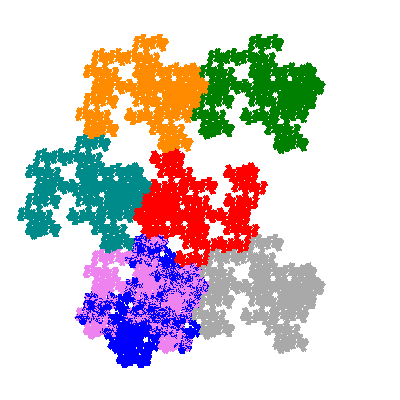
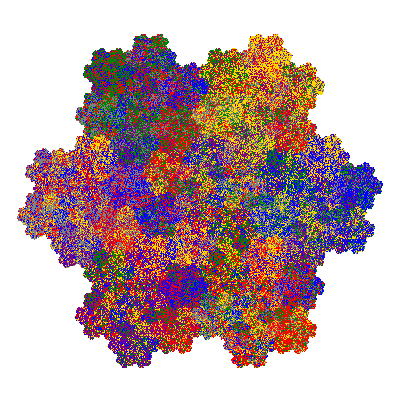
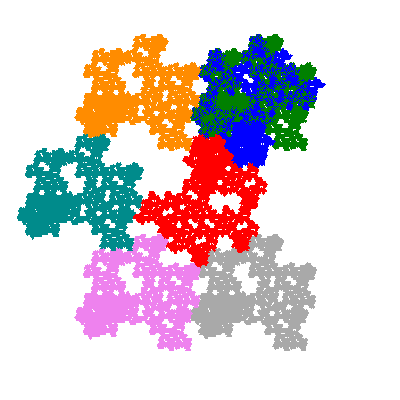
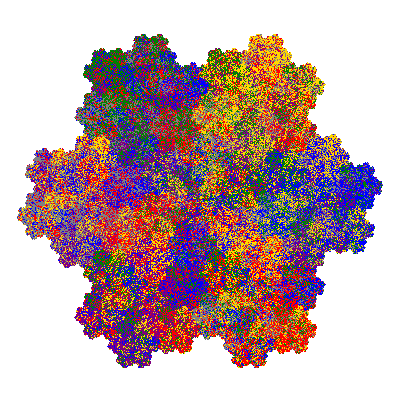
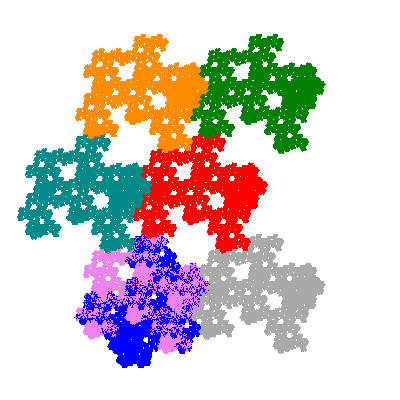
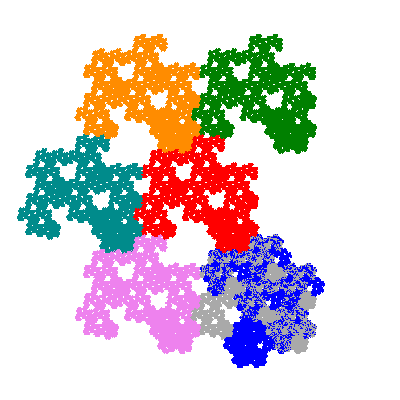
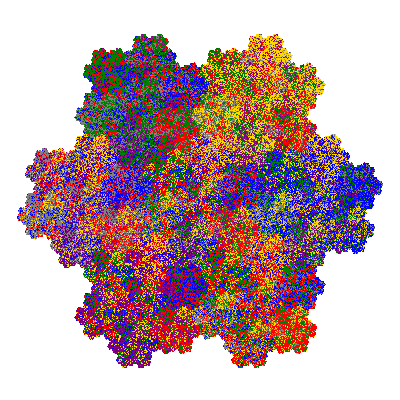
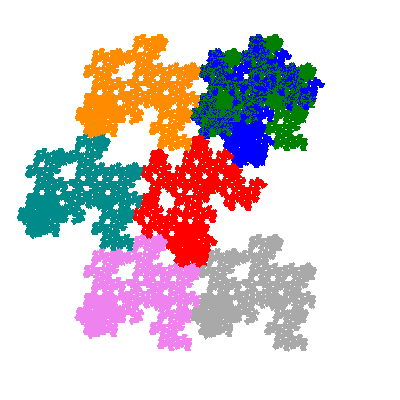
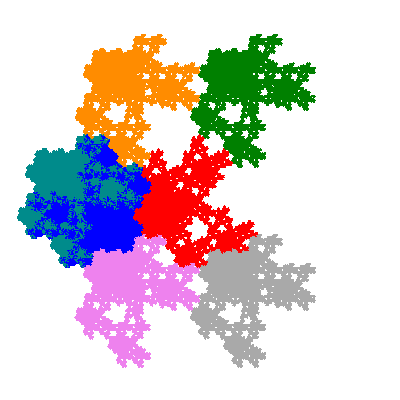
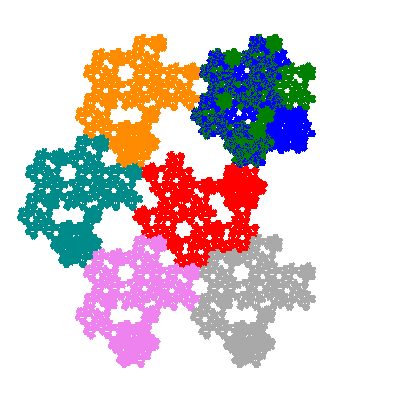
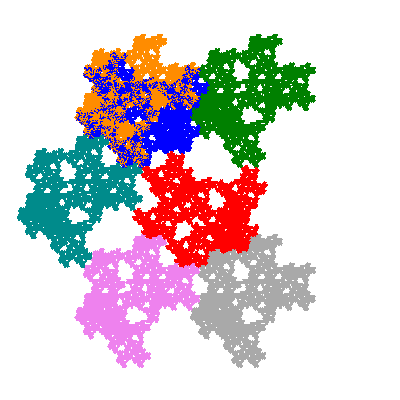
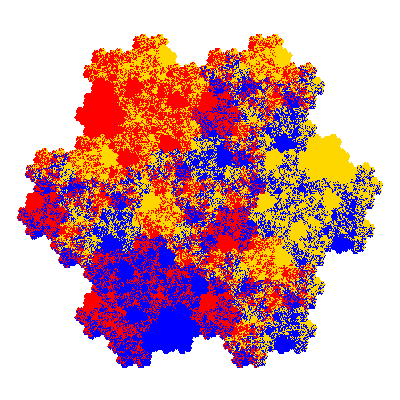
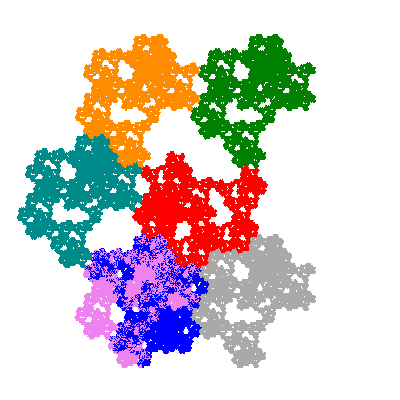
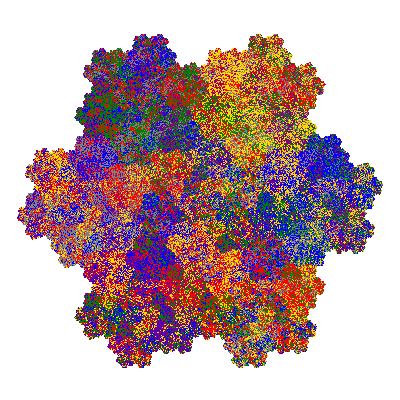
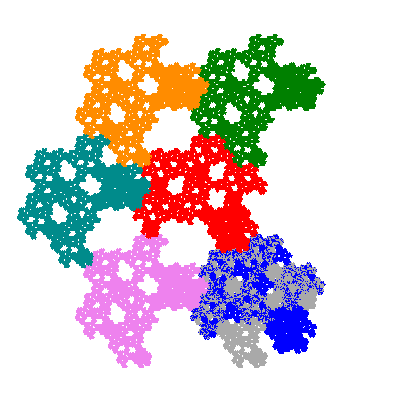
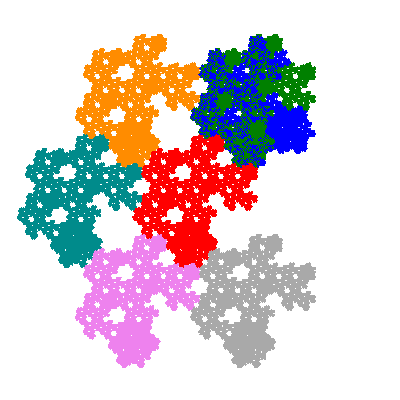
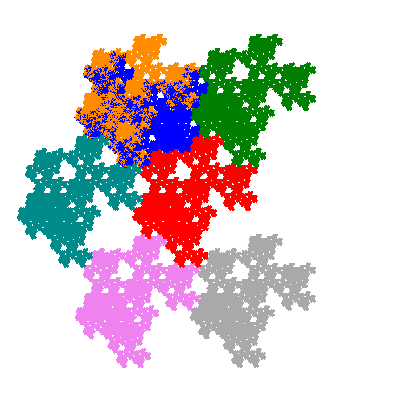
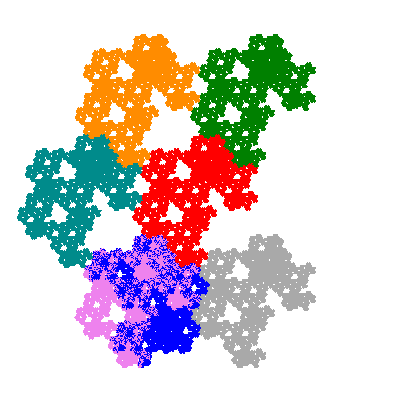
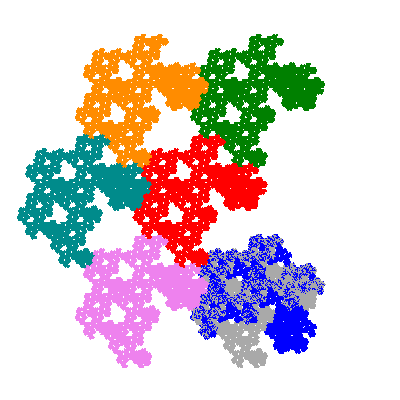
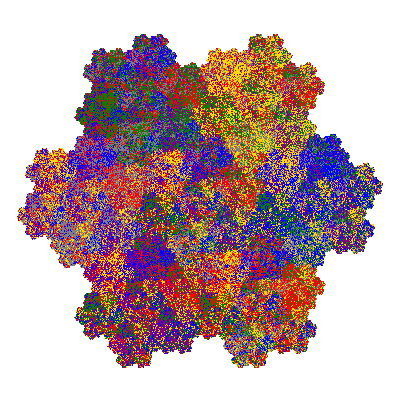
Source: Independent invention

© 2016 Stewart R. Hinsley