Flowsnakes

The names flowsnake, Gosper island, Gosper curve and Peano-Gosper curve have been applied to the directly self-similar cyclic heptahextal. I extend the name to include the corresponding inversely self-similar tile, distinguishing them as the cis-flowsnake and the trans-flowsnake.

The elements of the above figures can be considered as centred on 7 points of a hexagonal grid (e.g. at the Eisenstein integers e₀₀, e₁₀, e₁₁, e₀₁, -e₁₀, -e₁₁ and -e₀₁). I extend the concept of a fudgeflake to include additional c3-symmetric order 3n²+3n+1 tiles formed from elements forming a d6-symmetric hexagonal array with n+1 elements on each side, particularising these as the n^th order cis- and trans-fudgeflakes. These can equivalently by conceived of as being formed by adding elements (and reducing the size of each element to compensate) at the points on the hexagonal grid forming a ring around the points involved in the previous order tiles.

I conjecture that these two series of tiles have a countably infinite number of members, as there is no obvious reason why the construction should stop working at any point.

Each element of an n^th order flowsnake is contracted by √(3n²+3n+1) and rotated by arctan(n.sin(π/3)/(1+1.5n)) relative to the overall figure.

These obviously tile the plane with one copy in the unit cell. With the above orientations and placement of elements on a unit grid the tiling vectors are e_n0 + e_nn + e₁₁ and e_n0 + e₁₀ - e_0n.

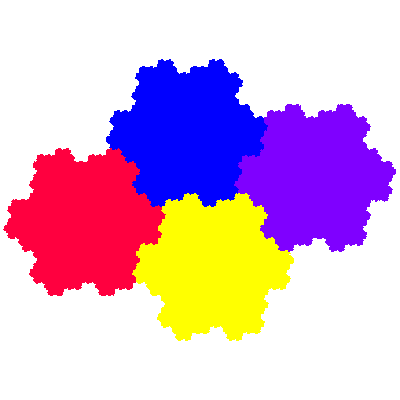
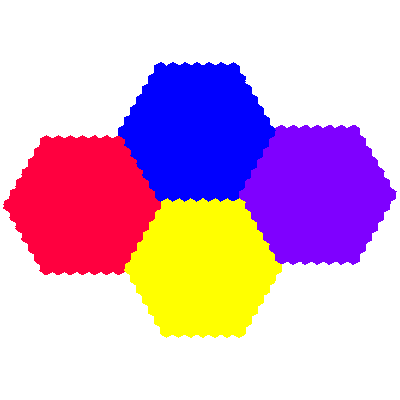
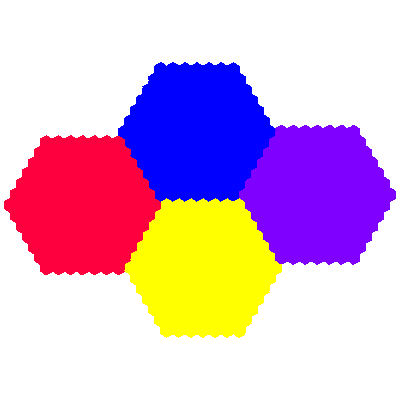
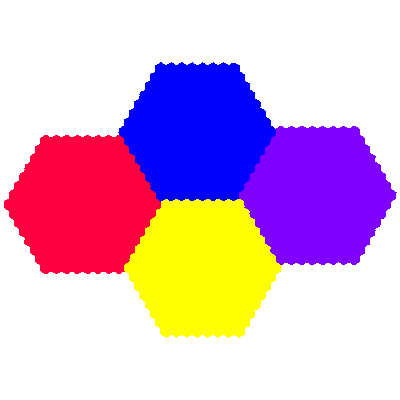
Source: All are independently discovered, except that the angle by which the elements of the cis 1st order flowsnake are rotated was derived from an L-system construction given in Scientific American.

© 2000, 2017, 2018 Stewart R. Hinsley