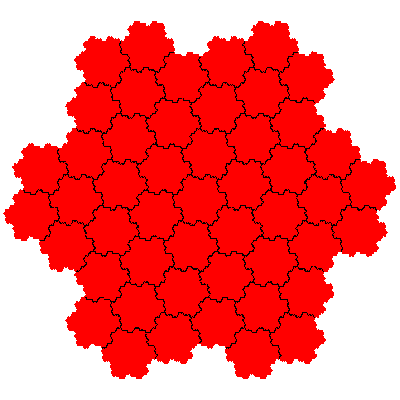

In the case of flowsnakes composition of IFSs generates new tiles for the combination of the cis- and trans-flowsnakes of a particular order.
The number of elements increases rapidly. There are two novel tiles with 49 (72) elements, 6 with 343 (73) elements, and 2 with 361 (192) elements. Assuming that the construction remains productive there are 2 with 1369 (372) elements, 12 with 2401 (74) elements, 2 with 6561 (812) elements, 6 with 5859 (193) elements, and so on. Composing flowsnakes of different orders gives 8 tiles with 133 (7×19) elements, 8 with 259 (7×37) elements, and so on.
If the cis-flowsnakes are denoted Gn and the trans-flowsnakes Gn then the order 49 tiles are G1.G1 and G1.G1.


The order 133 tiles are G1.G2, G2.G1, G1.G2, G2.G1, G1.G2, G2.G1, G1.G2 and G2.G1.

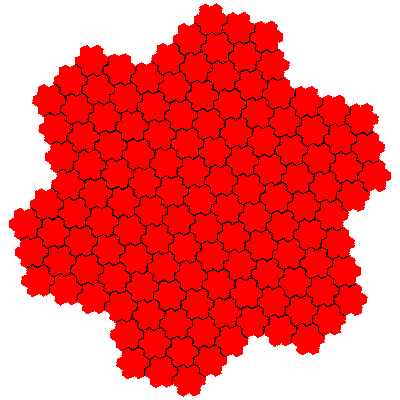

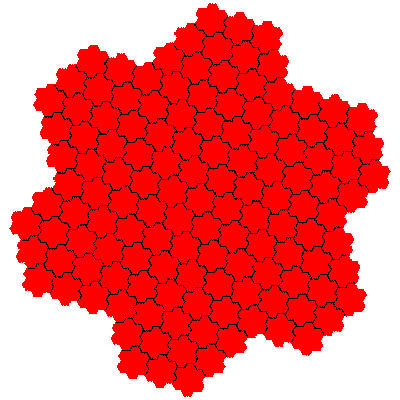
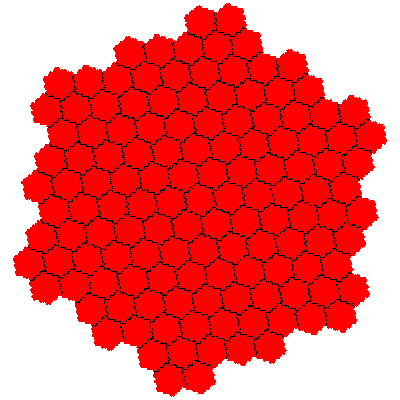
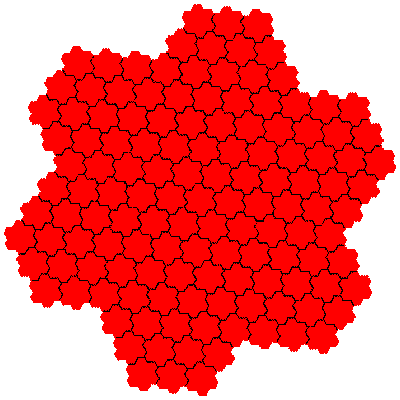
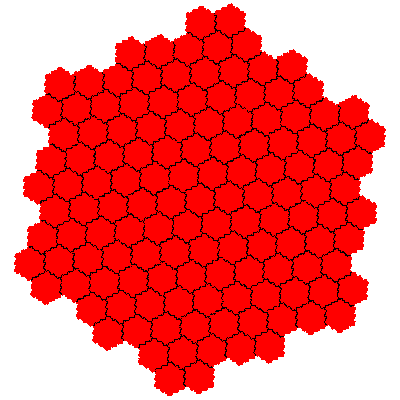
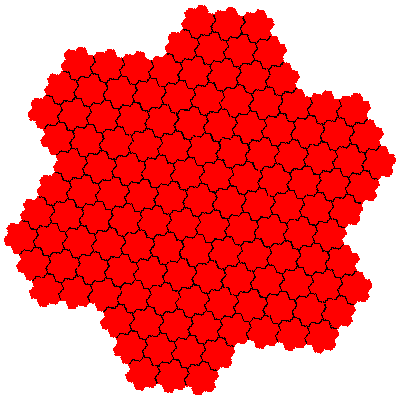
The order 343 tiles are G1.G1.G1, G1.G1.G1, G1.G1.G1, G1.G1.G1, G1.G1.G1 and G1.G1.G1.






The order 361 tiles are G2.G2 and G2.G2.


© 2017, 2018 Stewart R. Hinsley